Approximating π, part 2
Last time we met, we found a Taylor series for the arctangent function, and we used the fact that π = 4 arctan(1) to find approximations to π. Unfortunately, this representation had really poor convergence behavior, because 1 is way the hell out at the edge of the interval of convergence for this series. I’m loath to abandon a fun trick, though; is there a way we can iterate on this idea?
Approximating π better
When I start thinking about π, I start thinking about radians. For instance, I know that $\tan\left(\frac\pi4\right)= 1$. Therefore, $\pi = 4\arctan(1)$, but that fact wasn’t very helpful.
Another fact I know about the unit circle is that $\tan\left(\dfrac\pi6\right) = \dfrac{1}{\sqrt{3}}$. Therefore, $\pi = 6 \arctan\left(\dfrac{1}{\sqrt{3}}\right)$. I think this might yield a better approximation: I know off the top of my head1 that $\frac{1}{\sqrt{3}}$ is like 0.6, so it’s substantially in the interior of the interval of convergence. Let’s see how this works out; note that for algebra reasons I wish to write $\frac{1}{\sqrt{3}}$ as $3^{-1/2}$.
\[\begin{align*} \pi = 6\arctan\left(3^{-1/2}\right) &= 6 \cdot \displaystyle\sum_{k=0}^\infty (-1)^k\cdot \dfrac{1}{2k+1} \cdot \left(3^{-1/2}\right)^{2k+1} \\ &= 6 \cdot \displaystyle\sum_{k=0}^\infty (-1)^k \cdot \dfrac{1}{2k+1} \cdot 3^{-k-1/2} \\ &= 6 \cdot \displaystyle\sum_{k=0}^\infty (-1)^k \cdot \dfrac{1}{2k+1} \cdot \underbrace{\dfrac{1}{3^k}}_{!!!}\cdot\dfrac{1}{\sqrt{3}} \end{align*}\]I’m already lots happier with this representation, because look at that $3^k$ in the denominator; very beautiful, very powerful. This is going to converge way faster. Let’s also factor out that constant at the end:
\[\pi = 6\arctan(3^{-1/2}) = 2\sqrt{3} \cdot \displaystyle\sum_{k=0}^\infty (-1)^k \cdot \dfrac{1}{2k+1} \cdot \dfrac{1}{3^k}.\]The alternating series error bound
Happily, this is still an alternating series, so we can still use the alternating series error bound to easily find reasonably tight2 bounds on the truncation error. In this case, we find that:
\[|\pi - S_n| < \dfrac{2\sqrt{3}}{3^{n+1}\cdot(2n+3)}\]I could try to set this equal to whatever I want my error bound to be and solve for $n$, but unfortunately anything that looks like $b^n\cdot n$ isn’t going to have nice solutions. Therefore, more fun approaches are to spreadsheet this to death and/or to look at a graph of this function:
| k | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| error bound | 3.464102 | 0.384900 | 0.076980 | 0.018329 | 0.004752 | 0.001296 |
Here’s a graph:
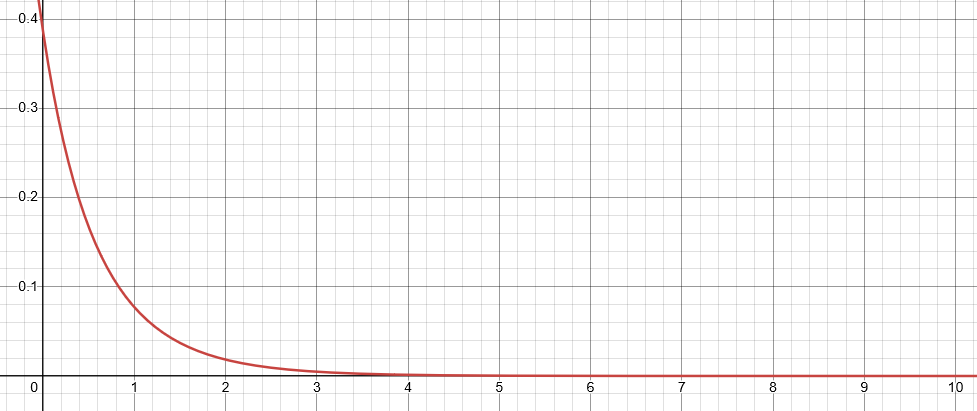
As you can see, those outputs get real small real quick; a graph on a logarithmic scale may be a better choice:
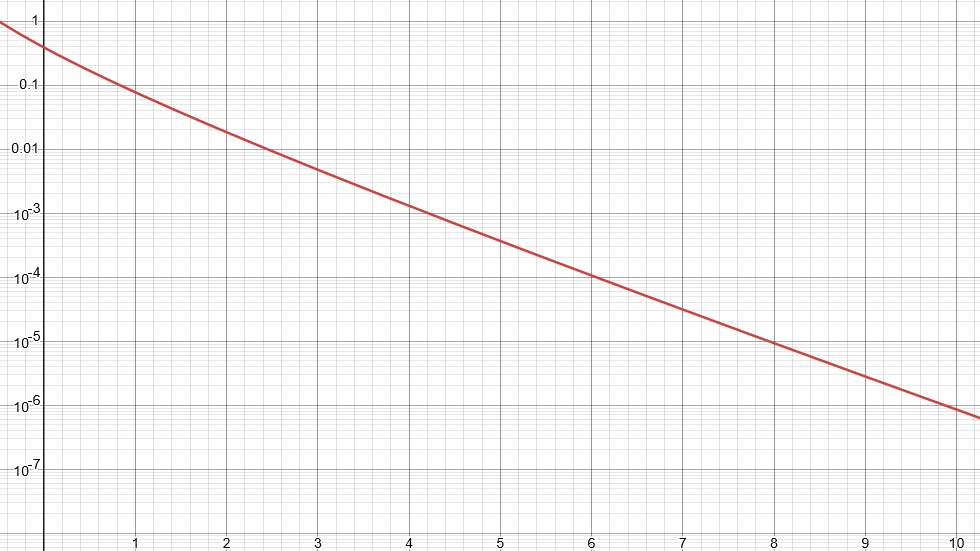
Hell yeah, these error bounds kick ass. I’m already down to $10^{-6}$ by the tenth term! Let us therefore compute a few approximations of π; here’s the first ten, rounded to the sixth decimal place:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| π ≈ | 3.464102 | 3.079201 | 3.156181 | 3.137853 | 3.142605 | 3.141309 | 3.141674 | 3.141569 | 3.141600 | 3.141591 |
This is much better, and much more fun, than the approximations we were getting before.
However…
We got into this whole mess by trying to figure out a way to approximate the transcendental number π, and we’ve done a pretty nice job. There’s a sneaky circular problem here, though: When we wrote
\[\pi = 6\arctan(3^{-1/2}) = 2\sqrt{3} \cdot \displaystyle\sum_{k=0}^\infty (-1)^k \cdot \dfrac{1}{2k+1} \cdot \dfrac{1}{3^k}\]as a way to approximate the transcendental number π, we used the irrational number $\sqrt{3}$.
How do you know what $\sqrt{3}$ is?
