Which country on Earth has the most people? If you guess China and India, in that order, you’d be right. And by a lot compared to other countries. A very distant third is the United States, with several countries close on our heels. Here are the population and growth rates estimates made in 2011.
| 1. |
China |
population 1.343 billion |
growth rate 0.48% |
| 2. |
India |
population 1.205 billion |
growth rate 1.31% |
| 3. |
United States |
population 0.313 billion |
growth rate 0.90% |
India’s population is growing fastest of these top three, so let’s take a closer look. In the exercises you can explore China and other countries. Let’s tackle this question: when is India’s population projected to pass 1.5 billion?
Start by writing an equation. The variables are
\begin{align*}
P \amp= \text{ population of India (billion people) } \sim \text{ dep} \\
Y \amp= \text{ time (years since 2011) } \sim \text{ indep}
\end{align*}
Since there is a fixed percentage growth, or at least that’s what we’re assuming, the population grows exponentially. The template for an exponential equation is
\begin{equation*}
\text{dep} = \text{start} \ast \text{growth factor} ^ {\text{indep}}
\end{equation*}
For India’s population, we know that the growth rate is
\begin{equation*}
r=1.31\% = \frac{1.31}{100} = 1.31 \div 100 = 0.0131
\end{equation*}
so the corresponding growth factor is
\begin{equation*}
g=1+r=1+0.0131=1.0131
\end{equation*}
We also know that the starting population is 1.205 billion in 2011. We’re good to go. The equation is
\begin{equation*}
P = 1.205 \ast 1.0131^Y
\end{equation*}
We want to know when India’s population will pass 1.5 billion people. That means we are looking for the value of
\(Y\) that corresponds to
\(P=1.5\text{.}\) That answer is called the
solution of our equation. In other words, a solution to an equation is the value of the independent variable we plug in to get the desired value of the dependent variable. It’s not always easy to
find a solution; but it’s easy to
check - just evaluate.
Since we can easily check and see if any number is a solution, one way to find the solution is to guess and check. Let’s try that to determine when India’s population will pass 1.5 billion people. Since we’re not sure where to start, let’s see what the equation projects for 2012, when \(Y=1\text{.}\)
\begin{equation*}
P=1.205 \ast 1.0131^1 = 1.205 \times 1.0131 \wedge \underline{1} = 1.2208096\ldots \approx 1.221 \text{ billion}
\end{equation*}
Hardly budged. Well, comparatively.
What about in 5 years? The corresponding population is
\begin{equation*}
P=1.205 \ast 1.0131^5 = 1.205 \times 1.0131 \wedge \underline{5} = 1.28614961\approx 1.286\text{ billion}
\end{equation*}
Less than 1.5 billion. Let’s try \(Y=10\text{.}\) The equation gives us
\begin{equation*}
P=1.205 \ast 1.0131^{10} = 1.205 \times 1.0131 \wedge \underline{10} = 1.37276417 \approx 1.373 \text{ billion}
\end{equation*}
Still much less than 1.5 billion
This is going slowly. We would really like to find a point at which the equation gives us more than 1.5 billion. Then we can work backwards from there to narrow things down. How about 50 years?
\begin{equation*}
P=1.205 \ast 1.0131^{50} = 1.205 \times 1.0131 \wedge \underline{50} = 2.31223244 \approx 2.312\text{ billion}
\end{equation*}
That’s too much, but the good news is now we know the solution is between 10 years and 50 years.
Let’s summarize what we have so far in a table. Notice how we’ve added a third row to keep track of our progress for our goal.
| \(Y\) |
0 |
1 |
5 |
10 |
50 |
|
|
|
|
| \(P\) |
1.205 |
1.221 |
1.287 |
1.373 |
2.312 |
\(\fillinmath{\displaystyle\int\int\int}\) |
\(\fillinmath{\displaystyle\int\int\int}\) |
\(\fillinmath{\displaystyle\int\int\int}\) |
\(\fillinmath{\displaystyle\int\int\int}\) |
| vs. 1.5 |
low |
low |
low |
low |
high |
\(\fillinmath{\displaystyle\int\int\int}\) |
\(\fillinmath{\displaystyle\int\int\int}\) |
\(\fillinmath{\displaystyle\int\int\int}\) |
\(\fillinmath{\displaystyle\int\int\int}\) |
We know the solution is between 10 and 50 years, and it seems closer to 10, so let’s guess 20 years. In 20 years, the population should be around 1.564 billion. Where’s that 1.564 from? Just our equation again. It would be good practice for you to evaluate at
\(Y=20\) to check.
The 10 year estimate is too low and the 20 year estimate is too high. That means the solution is between 10 years and 20 years, so let’s split the difference and guess 15 years which gives 1.465 billion. (Check again, for practice.) Ooooh, we’re getting close. The population should pass 1.5 billion some time between 15 and 20 years, and likely closer to 15 so let’s guess 17 years. Estimate is 1.504 billion. Would 16 years have been enough? That gives 1.484 billion, not quite enough. Let’s add these numbers to our table.
| \(Y\) |
0 |
1 |
5 |
10 |
50 |
20 |
15 |
17 |
16 |
| \(P\) |
1.205 |
1.221 |
1.287 |
1.373 |
2.312 |
1.564 |
1.465 |
1.504 |
1.484 |
| vs.1.5 |
low |
low |
low |
low |
high |
high |
low |
high |
low |
According to our equation, the population of the India should pass 1.5 billion after 17 years, which would be in the year 2028. By the way, it works to add the year and number.
\begin{equation*}
2011 + 17 \text{ years } = 2028
\end{equation*}
The strategy we used to find the solution of our equation is
successive approximation. Essentially it’s just the guess and check method, but it’s called “successive” because we’re trying to get a closer guess each time. Typically once we have a value that’s too big and one that’s too small, we guess a value in between (for example, their average). This sort of splitting the difference method of guessing is a rough version of the
bisection method. Now you know.
You might be surprised that you’re supposed to guess the solution at this point in the course. I mean, in the beginning of the course we didn’t have equations, just tables and graphs, and so guessing was all we had to work with. But now we have actual equations, right? In previous courses your instructor or textbook might have emphasized getting the “exact” solution.
Here’s why it’s different in this course. First, in almost every story in this book the numbers in the problem are approximations, or at least rounded off. If you start with approximations, no matter how exact your mathematics is, the solutions will still be approximate. Second, even if our numbers started out precisely exact, chances are that the equation is only approximating reality. Do we really know what the population growth rate will be in India over the next twenty years? And, if the equation is just approximate, then no matter how exact the numbers or the mathematics, the solution will again still be approximate. Last, and this is good news - we really just want approximations. Do you really need to know that a sandwich has 427.2889 calories? Isn’t 430 calories close enough? (Sound familiar? These ideas were discussed in more detail in
Prelude: Approximation & rounding.)
In previous mathematics courses you may have seen ways to solve equations “exactly,” and we will talk about those methods in the next chapters of this text. It is true that successive approximations can take a long time and, because of that, is a bit annoying. Solving techniques we’ll learn later are much, much quicker.
There are two important reasons for using successive approximations, even if you know quicker solving techniques. First, the method of successive approximations works in most situations for any type of equation. Solving methods that we will see later on just work for one type of an equation or another - one technique for linear equations, a different technique for exponential equations, etc. That’s a lot of different methods to know. Second, even if you’re going to use a formal equation-solving technique to solve a problem it’s a good habit to guess-and-check a bit first to make sure your solution is reasonable. It is easy to make mistakes when using those formal techniques. Remember,
I’d rather be approximately right than precisely wrong.
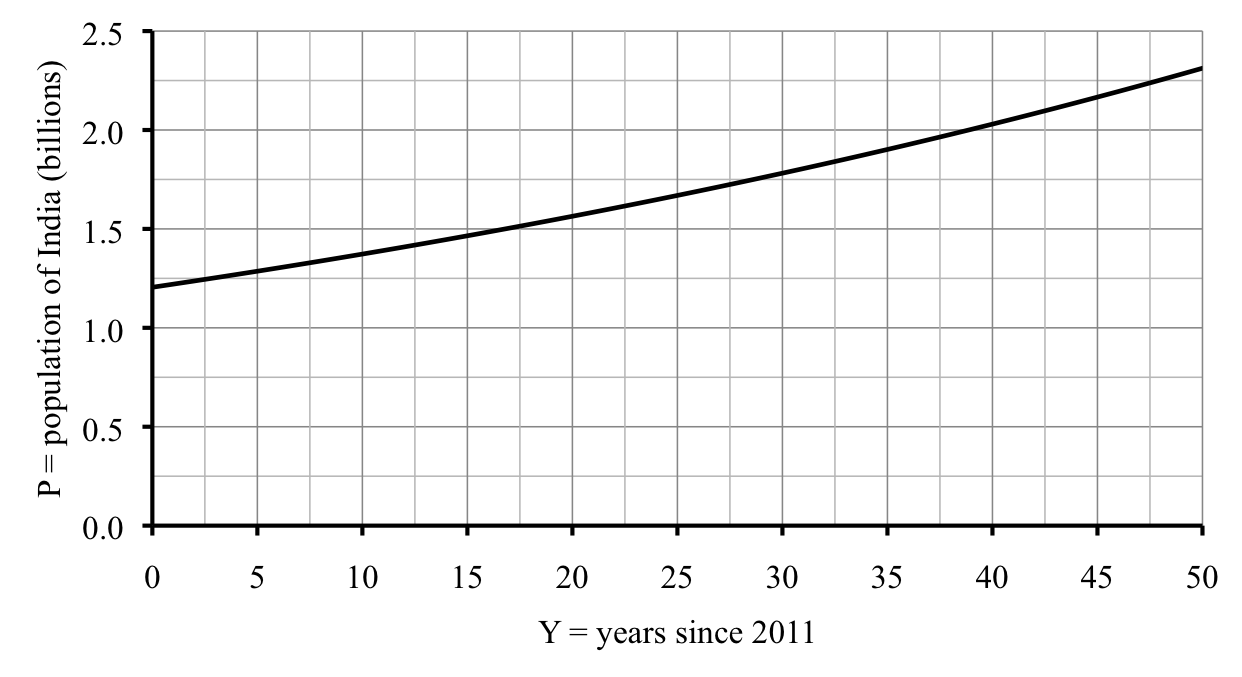
Okay, enough digression. Let’s check our answer using the graph.
It looks like 1.5 billion corresponds to just before the unlabeled gridline halfway between 15 and 20. That line would be 17.5, so the answer of 17 (which was year 2028) looks perfect.