A family with one full-time worker earning minimum wage cannot afford the local fair-market rent for a two-bedroom apartment anywhere in the United States. Even families earning above minimum can struggle to rent an apartment for less than 30% of their income. As a result, many people need affordable housing. There are various local, state, and federally funded programs as well as non-profit agencies working to increase availability.
In our city there are about 64,100 apartments considered affordable. So the city partnered with local developers to build 7,800 more apartments each year. Our variables are
\begin{align*}
A \amp= \text{ affordable housing (apartments) } \sim \text{ dep} \\
Y \amp= \text{ time (years from now) } \sim \text{ indep}
\end{align*}
Assuming things proceed as planned, after 5 years there would be
\begin{equation*}
64{,}100 \text{ apts } + 5 \text{ years} \ast \frac{7{,}800 \text{ apts}}{\text{year}}=64{,}100+\underline{5} \times 7{,}800 = 103{,}100 \text{ apartments}
\end{equation*}
Generalizing, we get our equation
\begin{equation*}
64{,}100+Y\ast 7{,}800 = A
\end{equation*}
which can be rewritten as
\begin{equation*}
A = 64{,}100 + 7{,}800Y
\end{equation*}
This equation fits our template for a linear equation
\begin{equation*}
\text{dep }=\text{ start } + \text{slope} \ast {\text{indep}}
\end{equation*}
Quick recap. A function is linear if its graph is a straight line, and nonlinear otherwise. The rate of change measures the steepness of the graph for any function, but a straight line is the same steepness everywhere, so the rate of change, or slope of a line is constant. Our example is linear because the slope of apartments per year is constant. Our starting or fixed amount is the intercept. In our example it’s apartments. The dependent variable and the intercept always have the same units - apartments in our example. But
\begin{equation*}
\text{units for slope} =\frac{\text{units for dep}}{\text{units for indep}}
\end{equation*}
so, in our example slope is measured in apartments per year. These units can help you identify the slope and intercept in a story - so keep a look out.
How many years will it take the city to reach 150,000 apartments at this rate? After ten years, for example, there would still not be enough affordable apartments because
\begin{equation*}
A = 64{,}100+7{,}800 \ast 10 = 64{,}100+ 7{,}800\times \underline{10}= 142{,}100 \text{ apartments}
\end{equation*}
Continuing successive approximation we get
| \(Y\) |
0 |
5 |
10 |
11 |
12 |
| \(A\) |
64,100 |
103,100 |
142,100 |
149,900 |
157,700 |
| vs. 150,000 |
low |
low |
low |
low |
high |
This city will reach 150,000 affordable apartments within 12 years.
Of course, we could solve a linear equation instead. We want \(A=150{,}000\text{.}\) Using our equation \(A=64{,}100 + 7{,}800 Y\) we get
\begin{equation*}
64{,}100 + 7{,}800Y = 150{,}000
\end{equation*}
However, since we want at least 150,000 affordable apartments, an inequality is even better. Let’s practice that.
\begin{equation*}
64{,}100 + 7{,}800Y \ge 150{,}000
\end{equation*}
Subtract from each side to get
\begin{equation*}
\begin{array}{lcr}
\phantom{-}\cancel{64{,}100} + 7{,}800 Y \amp \geq \amp 150{,}000 \\
-\cancel{64{,}100} \amp \amp -64{,}100
\end{array}
\end{equation*}
which simplifies to
\begin{equation*}
7{,}800Y\ge 85{,}900
\end{equation*}
Divide each side by 7,800 to get
\begin{equation*}
\frac{\cancel{7{,}800}~Y}{\cancel{7{,}800}} \ge \frac{85{,}900}{7{,}800}
\end{equation*}
which simplifies to
\begin{equation*}
Y \ge \frac{85{,}900}{7{,}800} = 85{,}900 \div 7{,}800 = 11.0128205\ldots
\end{equation*}
To be sure \(Y \ge 11.0128205\ldots\) we need to round up to get
\begin{equation*}
Y \ge 12
\end{equation*}
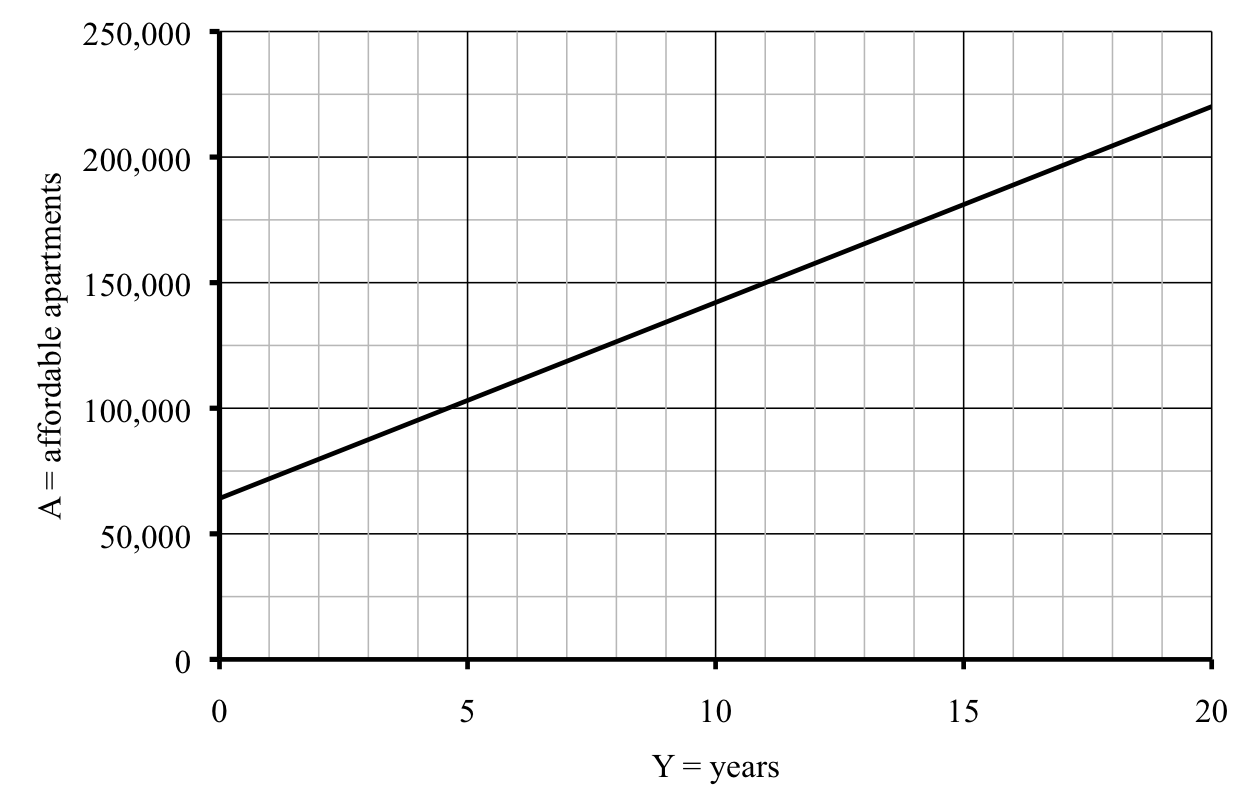
Let’s confirm our findings on the graph.
As expected, the graph is a straight line. And we see that the city should reach its goal of 150,000 affordable apartments in 12 years, or slightly before then.