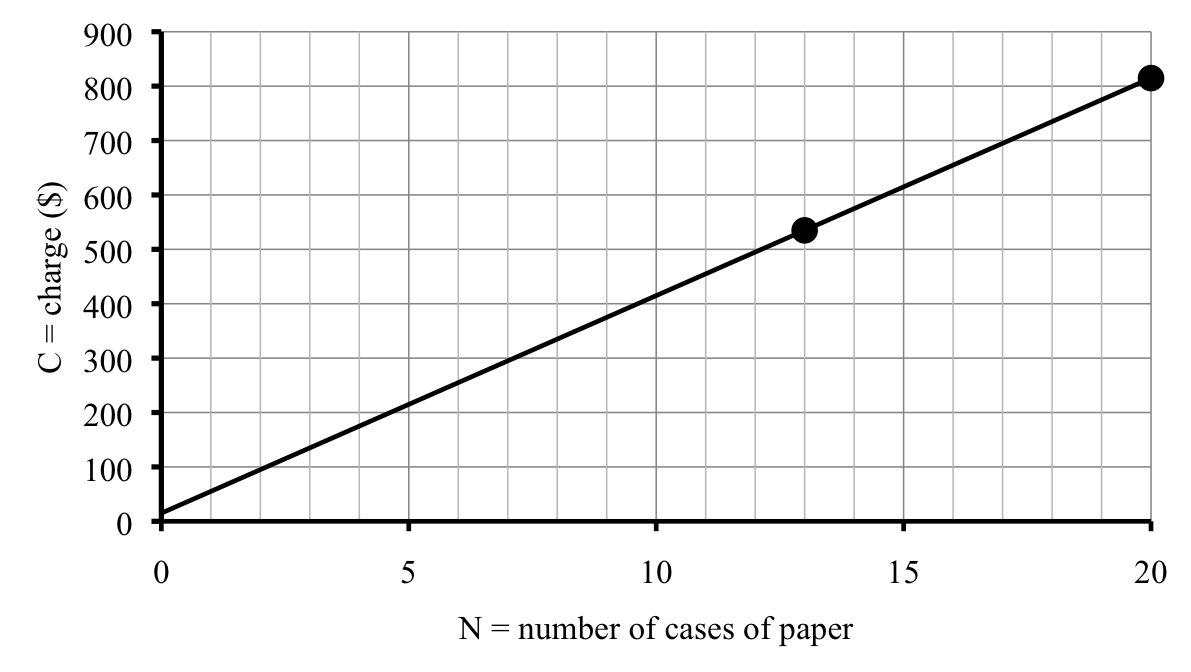
Last week our supplier delivered 13 cases of paper for the office and charged us $534.87. This week, they delivered 20 cases of paper for $814.80. We assume that their charge includes a fixed delivery fee and per case cost, so the dependence must be linear. We would like to understand their pricing scheme better by writing the equation.
What to do? We can name the variables and put the information we are given into a table. That’s a start. The variables must be
\begin{align*}
C \amp= \text{ total charge (\$) } \sim \text{ dep} \\
N \amp= \text{ number of cases delivered (cases) } \sim \text{ indep}
\end{align*}
and we know
| \(N\) |
13 |
20 |
| \(C\) |
534.87 |
814.80 |
Let’s see. The fixed delivery fee that we don’t know is the intercept. The per case cost that we also don’t know is the slope. To write the linear equation we need to know both.
The slope is just the rate of change, so we can figure out the slope just from the information in our table.
\begin{align*}
\text{slope} \amp = \text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{\$814.80-\$534.87}{20\text{ cases}-13 \text{ cases}} \\
\amp = \frac{\$279.93}{7 \text{ cases}} = 279.93 \div 7 = \$39.99 \text{ per case}
\end{align*}
or, all at once, as
\begin{align*}
\text{slope} \amp = \text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{\$814.80-\$534.87}{20\text{ cases}-13 \text{ cases}} \\
\amp = (814.80-534.87)\div(20-13)= \$39.99 \text{ per case}
\end{align*}
Either way, each case costs $39.99 and the slope is $39.99 per case.
Now that we know the slope, we can find the intercept. At $39.99 per case we would expect 13 cases to cost
\begin{equation*}
13 \text{ cases } \ast \frac{\$39.99}{\text{case}} = 13 \times 39.99 = \$519.87
\end{equation*}
But the story tells us 13 cases cost $534.87. The difference \(\$534.87 - \$519.87 = \$15\) must be the delivery fee which is the intercept. Remember
\begin{equation*}
\text{intercept} = \text{dep} -\text{slope}\ast\text{indep}= 534.87 - 39.99\times 13= \$15
\end{equation*}
Why did we use 13 cases instead of 20 cases? No particular reason. Look what happens if we use 20 cases at $814.80 instead.
\begin{equation*}
\text{intercept} = \text{dep} -\text{slope}\ast\text{indep}= 814.80 - 39.99\times 20= \$15
\end{equation*}
Yup. Still $15 delivery fee.
The equation is linear so it fits our template
\begin{equation*}
\text{dep} = \text{start} + \text{slope} * \text{indep}
\end{equation*}
and now that we know the slope and intercept, we can put those in to get our equation.
\begin{equation*}
C = 15 + 39.99N
\end{equation*}
Let’s check. When \(N = 13\) we get
\begin{equation*}
C=15 + 39.99 \ast 13 = 15 + 39.99 \times \underline{13} = \$534.87 \quad \checkmark
\end{equation*}
and when \(N=20\) we get
\begin{equation*}
C=15 + 39.99 \ast 20 = 15 + 39.99 \times \underline{20} = \$814.80 \quad \checkmark
\end{equation*}
You can also check that the graph goes through the original two points we were given. The intercept is $15, but because of the scale it shows up as barely above $0 on our graph.
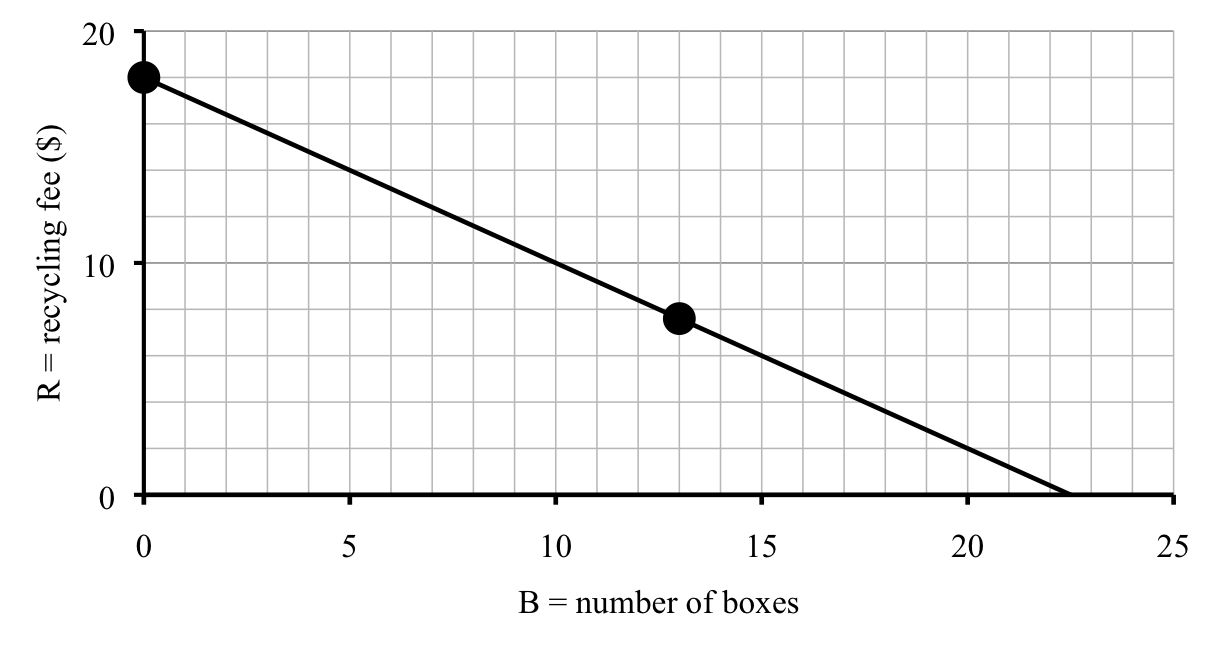
The supplier also picks up recyclable paper and boxes. They normally charge $18 per pickup but under a new reuse incentive program, they discount a little for each box that’s in good enough condition to use again. This week’s recycling charge was only $7.60 because we returned the previous 13 boxes all in good shape.
Now we’re interested in how the recycling charge depends on the number of boxes in good condition that we return. The new variables are
\begin{align*}
R \amp= \text{ recycling charge (\$) } \sim \text{ dep} \\
B \amp= \text{ number of boxes returned (boxes) } \sim \text{ indep}
\end{align*}
and we know
See how we used
\(B=0\) for the situation where no boxes are returned? Clever.
We can draw the graph using just these two points. (But we’ll check later, once we have the equation, to be sure.)
Since there is a fixed discount per box, we again have a linear function. We know the intercept is the normal recycling fee of $18. We need to find the slope.
\begin{align*}
\text{slope} \amp = \text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{\$7.60-\$18}{13\text{ boxes}-0 \text{ boxes}} \\
\amp = (7.60-18)\div(13-0)= -\$0.80 \text{ per box}
\end{align*}
It might look funny to get a negative, but it’s to be expected. They are subtracting for each good box returned. The discount is 80¢ per box and so the equation is
\begin{equation*}
R = 18 - 0.8B
\end{equation*}
Check when \(B=13\) we have
\begin{equation*}
R = 18 -0.8*13 = 18-0.8 \times \underline{13} = \$7.60 \quad \checkmark
\end{equation*}
What’s the most boxes you could get credit for? Probably the most they discount is the full $18, which would mean that \(R=0\text{.}\) That means we want to solve \(18 -0.8B = 0\text{.}\) Check that we get \(B = 22.5 \text{ boxes}\text{,}\) which means that 22 boxes would be almost $0 and for 23 boxes, they should pick up for free. We can check that 22 boxes gives
\begin{equation*}
R = 18-0.8\ast22=18-0.8 \times \underline{22} = \$0.40
\end{equation*}
and 23 boxes gives
\begin{equation*}
R = 18-0.8\ast23=18-0.8 \times \underline{23} = -\$0.40 \implies \text{free}
\end{equation*}
Well, unless they’re nice and give us cash back.