A local factory produces small locks for industrial use. The old machine has seen better days and Quia Xun, the manager, is shopping around for a new machine. She’s narrowed it down to two options. The first option is replace the old machine with a new model (Machine 1) for $3,200. The second is a larger unit (Machine 2) priced at $5,400. In each case, the price includes installation and the standard service contract. The reason she is considering the more expensive machine is Machine 2 runs at a cost of only $0.80 per lock, whereas the replacement Machine 1 runs at a cost of $1.25 per lock.
Since Machine 1 is less expensive, Quia Xun knows it is the right choice if the factory only produces a small number of locks. But since Machine 2 costs less per lock to run, she knows it will pay off if the factory makes a large number of locks. She would like to understand the total expenditure better, particularly the number of locks at which it would be worthwhile to invest in the more expensive machine.
Since Quia Xun is interested in how the total expenditure, including both the purchase price and the running cost, depend on the number of locks produced, the variables are
\begin{align*}
L \amp= \text{ amount produced (locks) } \sim \text{ dep} \\
E \amp= \text{ total expenditure (\$) } \sim \text{ indep}
\end{align*}
She recognizes that total expenditure is a linear function that depends on the purchase price and the running cost for each machine. In each case, the starting amount (intercept) is the purchase price: $3,200 for Machine 1 and $5,400 for Machine 2. The slope (rate of change) is the constant running cost: $0.80 per lock for Machine 1 and $1.25 per lock for Machine 2. Using the template for a linear equation
\begin{equation*}
\text{dep }=\text{ start } + \text{ slope} \ast {\text{indep}}
\end{equation*}
she writes the equations
\begin{align*}
\textbf{Machine 1: } \qquad
E\amp= 3{,}200 + 1.25 L \\
\textbf{Machine 2: } \qquad
E\amp= 5{,}400 + 0.80 L
\end{align*}
Since there are two linear equations and we are interested in a comparison, we have a system (of linear equations).
To begin the comparison, Quia Xun starts with figuring out what the expenditure to produce 2,000 locks would be for each machine.
\begin{align*}
\textbf{Machine 1: } \qquad
E\amp= 3{,}200 + 1.25 \times \underline{2{,}000}=\$5{,}700 \\
\textbf{Machine 2: } \qquad
E\amp=5{,}400 + 0.80 \times \underline{2{,}000}=\$7{,}000
\end{align*}
If the factory were only going to make only 2,000 locks, then Machine 2 would not be worth it. She calculates a few more examples to see what the cutoff would be.
| \(L\) |
2,000 |
4,000 |
6,000 |
8,000 |
10,000 |
|
Machine 1: \(E\)
|
5,700 |
8,200 |
10,700 |
13,200 |
15,700 |
|
Machine 2: \(E\)
|
7,000 |
8,600 |
10,200 |
11,800 |
13,400 |
Even at 4,000 locks, Machine 1 is the better deal. By 6,000 locks, Machine 2 becomes the better deal. Somewhere in between it switches.
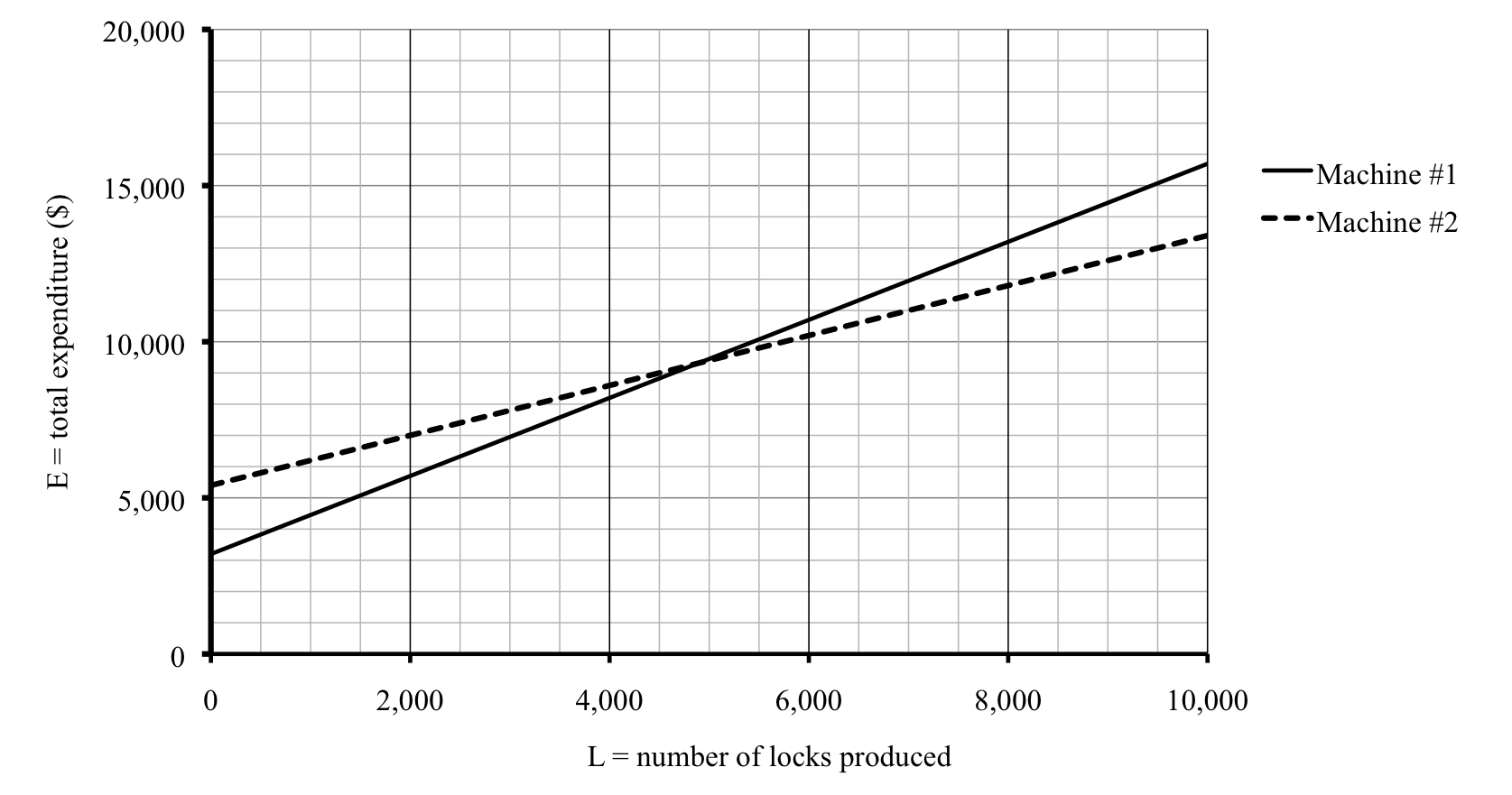
Quia Xun makes a quick graph to see what’s going on. On the graph, whichever line is lower corresonds to the lower total expenditure and whichever line is higher corresponds to the higher total expenditure. As suspected, for a smaller number of locks the line for Machine 1 is lower on the graph, so that’s the better deal. For a larger number of locks it switches and the line for Machine 2 is lower on the graph, since that’s the better deal instead. Where they switch corresponds to the point on the graph where the two lines cross, somewhere around 5,000 locks.
A quick successive approximation narrows down the answer.
| \(L\) |
4,000 |
6,000 |
5,000 |
4,500 |
4,800 |
4,900 |
|
\(E\) (for Machine 1) |
8,200 |
10,700 |
9,450 |
8,825 |
9,200 |
9,325 |
|
\(E\) (for Machine 2) |
8,600 |
10,200 |
9,400 |
9,000 |
9,240 |
9,320 |
| Less expensive option |
Machine 1 |
Machine 2 |
Machine 2 |
Machine 1 |
Machine 1 |
Machine 2 |
So the choice changes somewhere between 4,800 and 4,900 locks.
There is a way for Quia Xun to solve the problem symbolically; we refer to this process as solving the system. She wants to find the number of locks where
\begin{equation*}
E \text{ (Machine 1)} = E \text{ (Machine 2)}
\end{equation*}
Using her equations \(E =3{,}200 + 1.25L\) for Machine 1 and \(E =5{,}400 + 0.80L\) for Machine 2 she has
\begin{equation*}
3{,}200 + 1.25L=5{,}400 + 0.80L
\end{equation*}
She wants to find the value of \(L\) that makes both sides the same number. To solve, Quia Xun subtracts 3,200, the smaller of the two purchase prices, from each side to get
\begin{equation*}
\begin{array}{lcl}
\phantom{-}\cancel{3{,}200}+1.25L \amp = \amp \phantom{-}5{,}400+0.80L \\
-\cancel{3{,}200} \amp = \amp -3{,}200
\end{array}
\end{equation*}
which simplifies to
\begin{equation*}
1.25L = 2{,}200 + 0.80L
\end{equation*}
Pause for a minute. What does that $2,200 mean in the story? It’s the extra cost of buying Machine 2 because \(\$5{,}400 - \$3{,}200 = \$2{,}200\text{.}\)
What next? This equation has the variable \(L\) on each side. Quia Xun needs to combine them somehow. Here’s how to do that. Subtract \(0.80L\) from each side. Look closely. She is subtracting \(0.80L\text{,}\) not just \(0.80\text{.}\) We get
\begin{equation*}
\begin{array}{lcr}
\phantom{-}1.25L \amp = \amp 2{,}200 +\cancel{0.80L} \\
-0.80L \amp \amp -\cancel{0.80L}
\end{array}
\end{equation*}
How do we simplify \(1.25L-0.80L\text{?}\) Think about what these numbers represent in the story. The cost was $1.25 per lock versus $0.80 per lock. The difference is $1.25 - $0.80 = $0.45 per lock. So that means
\begin{equation*}
1.25L -0.80L = 0.45L
\end{equation*}
Think: 125 apples - 80 apples = 45 apples. She can now simplify her equation to get
\begin{equation*}
0.45L = 2{,}200
\end{equation*}
Ah, she can solve this equation just by dividing each side by 0.45 to get
\begin{equation*}
\frac{\cancel{0.45}L}{\cancel{0.45}}= \frac{2{,}200}{0.45}
\end{equation*}
which simplifies to
\begin{equation*}
L = \frac{2{,}200}{0.45}= 2{,}200 \div 0.45 = 4888.88888\ldots \approx 4{,}889 \text{ locks}
\end{equation*}
If they plan to produce 4,889 locks or more, Quia Xun should go ahead and buy the more expensive machine, Machine 2. Yeah, that’s what we guessed – just under 4,900 locks is the payoff.
She solved an equation here, but Quia Xun really wanted to know when
\begin{equation*}
E \text{ (Machine 1)} \geq E \text{ (Machine 2)}
\end{equation*}
so she could have solved the inequality
\begin{equation*}
3{,}200 + 1.25L \ge 5{,}400 + 0.80L
\end{equation*}
instead. Check that the same steps give
\begin{equation*}
L \ge 4{,}889 \text{ locks}\text{.}
\end{equation*}