Quadratic Equation Template
\begin{equation*}
\text{dep} = a \ast \text{indep}^2 + b \ast\text{indep} + c
\end{equation*}
Section 3.5 Solving quadratic equations
Claude likes to juggle. As he throws a beanbag up in the air, the height changes over time as described by the equation
\begin{equation*}
H = 3+15T-16T^2
\end{equation*}
where
\begin{align*}
H \amp= \text{ height of beanbag (feet) } \sim \text{ dep} \\
T \amp= \text{ time (seconds) } \sim \text{ indep}
\end{align*}
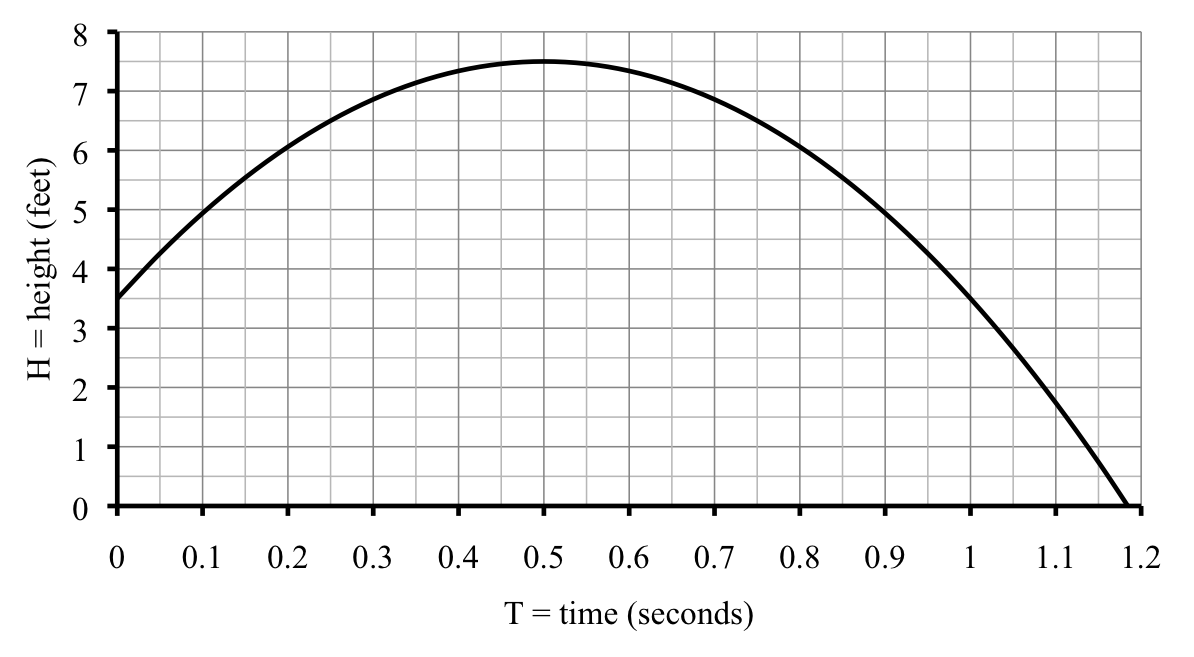
Let’s make a table and graph this function. For example, when \(T=0\) seconds we have
\begin{equation*}
H = 3 + 15 \ast 0-16 \ast 0^2 = 3 + 15 \times \underline{0} - 16 \times \underline{0} \wedge 2 = 3 \text{ feet}
\end{equation*}
and when \(T=1\) second we have
\begin{equation*}
H = 3 + 15 \ast 1-16 \ast 1^2 = 3 + 15 \times \underline{1} - 16 \times \underline{1} \wedge 2 = 2 \text{ feet}
\end{equation*}
Huh? I thought the beanbag went up in the air. What’s happening here? Oh, I know. The beanbag must be falling down by then. As we fill in the table with intermediate values we see how Claude’s beanbag went up in the air and then back down.
| \(T\) | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
| \(H\) | 3 | 4.34 | 5.36 | 6.06 | 6.44 | 6.50 | 6.34 | 5.66 | 4.76 | 3.54 | 2 | 0.14 | \(\cancel{-2.04}\) |
Notice by \(T=1.2\) seconds we got \(-2.04\) feet. We can’t have negative feet. The beanbag must hit the ground before 1.2 seconds. From the graph I’d say in just over 1.1 seconds.
Of course, we can refine our answer by successive approximations. The beanbag hits the ground when its height is 0 feet. Looks a little strange but we want \(H =0\text{.}\) We expect the answer is just a little bigger than 1.1, so we start our guess optimistically with 1.11.
| \(T\) | 1.1 | 1.11 | 1.105 | 1.107 | 1.106 |
| \(H\) | 0.14 | \(\cancel{-0.06}\) | 0.0368 | \(\cancel{-0.002}\) | 0.018 |
| vs. 0 | high | low | high | low | good |
The beanbag was in the air for approximately 1.106 seconds.
In this chapter we’ve seen how to solve linear, power, and exponential equations. Let’s solve this equation too. By the way, our function is quadratic because
\begin{equation*}
H = 3+15T-16T^2
\end{equation*}
fits the template for a quadratic equation.
with constants
\begin{equation*}
a = -16 \quad b = 15 \quad c = 3
\end{equation*}
(More on how we found those numbers in a moment.)
Back to our juggler. We are trying to figure out when \(H=0\text{.}\) Using our equation \(H=3+15T-16T^2\text{,}\) we get
\begin{equation*}
3+15T-16T^2=0
\end{equation*}
We want to solve for \(T\text{.}\) Notice that because \(T\) occurs twice in the equation, nothing we have seen to do to each side of the equation can knock it down to just one \(T\text{.}\) That means none of our methods so far work. Luckily there’s a way to solve any quadratic equation using the aptly-named Quadratic Formula.
Quadratic Formula
The equation \(aT^2+bT+c=0\) has solutions
\begin{equation*}
T = \frac{-b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a}
\end{equation*}
Oh my! First thing to understand in this complicated formula is that we actually get two possible answers
\begin{equation*}
T = \frac{-b}{2a}+ \frac{\sqrt{b^2-4ac}}{2a} \quad \text{and} \quad T = \frac{-b}{2a} - \frac{\sqrt{b^2-4ac}}{2a}
\end{equation*}
Sometimes one answer makes sense in the story, other times they both might. Stay tuned.
For Claude’s situation we had
\begin{equation*}
3+15T-16T^2=0
\end{equation*}
To fit the formula, we need the \(T^2\) first, the \(T\) second, and then the constant. No sweat, just reorder to get
\begin{equation*}
-16T^2 + 15T + 3=0
\end{equation*}
Notice how subtracting \(16T^2\) became adding \(-16T^2\) when we rearranged? That lines up perfectly with
\begin{equation*}
aT^2+bT+c=0
\end{equation*}
That’s how we knew the constants were
\begin{equation*}
a = -16 \quad b = 15 \quad c = 3
\end{equation*}
The first fraction in the formula is
\begin{equation*}
\frac{-b}{2a} = \frac{-15}{2\ast-16} = \text{(-)}15 \div (2 \times \text{(-)}16) = 0.46875
\end{equation*}
As usual, we needed parentheses around the denominator (bottom) of our fraction to override the normal order of operations. As a reminder, (-) refers to negation. Remember, this does not mean you type in parentheses, just hit the one key that is labeled already.
The second fraction is
\begin{align*}
\frac{\sqrt{b^2-4ac}}{2a} \amp = \frac{\sqrt{(15)^2-4 \ast -16 \ast 3}}{2 \ast-16}\\
\amp = \sqrt{~} ( (15) \wedge 2 - 4 \times \text{(-)}16 \times 3) \div (2 \times \text{(-)}16)\\
\amp = -0.6381431\ldots \approx -0.63814
\end{align*}
Check out the parentheses now. Three sets here. First, around the quantity we’re taking the square root of. Maybe your calculator included the open parentheses along with the square root, but either way we need them. Second, around the number (15) that we are squaring. That didn’t matter here but if \(b\) were negative it would have. Last, we added parentheses around the bottom of the fraction, as always.
Oh, and we’re not done yet. Remember there are two possible answers. One is the sum of these two numbers
\begin{equation*}
0.46875 + \text{(-)}0.43814 = -0.46939 \text{ seconds}
\end{equation*}
which doesn’t make any sense because time is never negative. The other is the difference
\begin{equation*}
0.46875 - \text{(-)}0.43814 = 1.10689 \text{ seconds}
\end{equation*}
We had guessed around 1.106 seconds, so that is definitely the right answer: Claude’s beanbag will hit the ground after 1.10689 seconds. Yeah, too precise. But you get the idea.
Wait a minute! Any good juggler isn’t about to let the beanbag fall on the ground. He’s going to catch it again, perhaps at about \(3\tfrac12\) feet above ground. That means we’re looking for \(H=3.5\text{.}\) Using our equation \(H=3+15T-16T^2\text{,}\) we get
\begin{equation*}
3+15T-16T^2=3.5
\end{equation*}
The Quadratic Formula only works if the equation has \(=0\text{,}\) but we have \(=3.5\text{.}\) It might seem that we’re out of luck, but it’s an easy fix. Just subtract 3.5 from each side.
\begin{equation*}
\begin{array}{lcr}
\phantom{-3.}3+1.5T-16T^2 \amp = \amp \cancel{3.5} \\
-3.5 \amp \amp -\cancel{3.5}
\end{array}
\end{equation*}
which simplifies to
\begin{equation*}
-0.5+15T -16T^2 = 0
\end{equation*}
So now we have \(=0\text{.}\) Yes!
We can write the new equation as
\begin{equation*}
-16T^2 + 15T -0.5= 0
\end{equation*}
from which we see that
\begin{equation*}
a = -16 \quad b = 15
\end{equation*}
as before, but now we have a new value
\begin{equation*}
c=-0.5
\end{equation*}
We’re all set to use the Quadratic Formula.
The first fraction is
\begin{equation*}
\frac{-b}{2a} = \frac{-(15)}{2 \ast -16} = \text{(-)}15 \div (2 \times \text{(-)}16) = 0.46875
\end{equation*}
No surprise here. We used the same values of \(a\) and \(b\) as before, so we should have the same number here. The second fraction is
\begin{align*}
\frac{\sqrt{b^2-4ac}}{2a} \amp= \frac{\sqrt{(15)^2-4 \ast -16 \ast -0.5}}{2 \ast-16}\\
\amp= \sqrt{~} ( (15) \wedge 2 - 4 \times \text{(-)}16 \times \text{(-)}0.5) \div (2 \times \text{(-)}16)\\
\amp= -0.43413887\ldots \approx -0.43414
\end{align*}
Don’t forget we need to put together these parts to find the possible answers. The sum gives us
\begin{equation*}
0.46875 + \text{(-)}0.43414 = 0.03461 \approx 0.03 \text{ seconds}
\end{equation*}
and the difference gives us
\begin{equation*}
0.46875 - \text{(-)}0.43414 = 0.90289 \approx 0.9 \text{ seconds}
\end{equation*}
Both answers seem to make sense. Let’s look at the graph to confirm that they’re reasonable. We first find \(H=3.5\) while the beanbag is going up in the air, just before the unlabeled gridline for 0.05 (midway between 0 and 0.1) so an answer of \(T\approx 0.03\) makes sense. Then, on the way back down, the beanbag is 3.5 feet up at what looks like 0.9 seconds, so our answer of \(T \approx 0.9\) makes sense too. Since Claude catches the beanbag on the way down, we want that second answer, after 0.90289 seconds (which is just before 1.106 seconds when it hits the ground, by the way).
One interesting note. What happens in the story at the point where the beanbag stops going up in the air and starts falling down? That must be when the beanbag is at its highest point. What is the speed at that highest point? Well, I guess 0. For a split second it’s almost frozen in midair, neither rising nor falling. (If we were able to compute the rate of change for a really, really small interval of time then we would find the rate of change \(\approx 0\text{.}\))
Turns out it’s easy to find that point for a quadratic equation, just plug in the first fraction from the Quadratic Formula! Check it out. When
\begin{equation*}
T = \frac{-b}{2a} = \frac{-15}{2 \ast -16}= \text{(-)}15 \div (2 \times \text{(-)} 16)= 0.46875 \text{ seconds}
\end{equation*}
we get
\begin{align*}
H \amp= 3 + 15 \ast 0.46875-16 \ast 0.46875^2\\
\amp= 3 + 15 \times \underline{0.46875} - 16 \times \underline{0.46875} \wedge 2\\
\amp= 6.515625\ldots \approx 6.516 \text{ feet}
\end{align*}
Claude throws the beanbag about 6.516 feet up. Converting to more normal units we get
\begin{equation*}
0.516 \cancel{\text{ feet}} \ast \frac{12 \text{ inches}}{\cancel{\text{ feet}}} = 0.516 \times 12 = 6.192 \approx 6 \text{ inches}
\end{equation*}
The beanbag goes up to about 6′6″. You can check that the graph shows just over 6.5 feet.
In general, the graph of \(H = aT^2+bT+c\) is a parabola. The two solutions from the Quadratic Formula are both places where \(H=0\) (we give them the fancy name roots) and, so, the graph crosses the \(T\)-axis there. Might not make sense in the real problem, but the equation and formula don’t know that. (Okay, equations and formulas don’t actually “know” anything. But you get my point.) Turns out the graph is symmetric about the highest point, so that must be midway in between the roots which is exactly where
\begin{equation*}
T =\frac{-b}{2a}
\end{equation*}
Because \(a\) is negative, the answer we got by adding is to the left and the answer we got by subtracting is to the right.
Our graph was a \(\cap\) shaped parabola and so we found a maximum value. The graph of a quadratic function might be \(\cup\) shaped instead. In that case evaluating at \(T=\frac{-b}{2a}\) would give the minimum value.
Do you know …
-
What a “quadratic” function is?
-
How to solve a quadratic equation?
-
When we use the Quadratic Formula? Ask your instructor if you need to remember the Quadratic Formula or if it will be provided during the exam.
-
How to solve a quadratic equation when the function is not set equal to zero?
-
How to identify the values of \(a, b, c\) in the formula?
-
How to evaluate the formula (using your calculator)?
-
Why there are (usually) two solutions to a quadratic equation?
-
How to decide which solution(s) from the Quadratic Formula are correct?
-
What the graph of a quadratic function looks like?
-
The value for the independent variable to find the highest (or lowest) value of a quadratic function?
If you’re not sure, work the rest of exercises and then return to these questions. Or, ask your instructor or a classmate for help.
Exercises Exercises
Exercises 1-4 are available in a separate workbook format.
1.
A high-jumper jumps so that the height, \(H\) feet, of the point on his back that must clear the bar after \(T\) seconds is given by the equation
\begin{equation*}
H = 3.5 + 16T -16T^2
\end{equation*}
(a)
When would the high-jumper hit the ground (if there were no pit)? Ouch! Use the Quadratic Formula to find the answer. Use the graph to check.
(b)
The high jump pit is 2 feet off the ground. When does the high-jumper land in the pit? Use the Quadratic Formula to find the answer and the graph to check.
(c)
How high a bar can the high-jumper clear? Find the maximum height of that point above ground by evaluating at \(\displaystyle T=\frac{-b}{2a}\text{.}\) Use the graph to check.
2.
The art museum opened in 1920. After an initial rush to see the great holdings, attendance dropped for awhile. But then attendance began to rise again and has risen since. The number of annual visits \(N\) is approximated by the equation
\begin{equation*}
N= 51T^2-840T+3{,}700
\end{equation*}
where \(T\) is time measured in years since 1920.
(a)
Calculate the missing values in the table.
| year | 1920 | 1925 | 1930 | 1935 | 1940 | 1945 | 1950 |
| \(T\) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| \(N\) | 3,700 | \(\fillinmath{\displaystyle\int\int\int}\) | 400 | 2,575 | 7,300 | \(\fillinmath{\displaystyle\int\int\int}\) | 24,400 |
(b)
Draw a graph of the function.
(c)
In what year did the number of visitors first pass 30,000 in a year? Estimate the value from your graph. Then set up and solve a quadratic equation.
(d)
According to this equation, in what year was the number of annual visits the smallest? For that year, what were the number of visits? Use \(\displaystyle T=\frac{-b}{2a}\text{.}\)
(e)
Explain why \(N\) never equals 0.
(f)
3.
The profit $\(P\) from selling \(M\) tanks of milk is described by the equation
\begin{equation*}
P=-2M^2+2{,}000M-80{,}000
\end{equation*}
(a)
Here is a graph of the function:
Explain why negative numbers on the vertical axis make sense in the story.
(b)
How much milk must be sold for the company to break even, meaning having $0 profit? Guess from the graph and check using the equation.
(c)
For practice, set up and solve a quadratic equation to find the break-even point.
(d)
How many tanks of milk would they need to sell to keep profits over $400,000? Set up and solve a quadratic equation to find the answer. Then check that it agrees with your graph. Your answer should be in the form of an inequality.
4.
Urban community gardens are catching on. What was once an abandoned lot down the block is now a thriving 10′\(\times\)25′ vegetable and berry garden for the neighborhood. One neighbor volunteered to donate gravel to make a path around the garden. The path will be 3 inches deep and the same width all around.
The amount of gravel we need (\(G\) cubic feet) is given by the equation
\begin{equation*}
G = W^2 + 17.5W
\end{equation*}
where \(W\) is the width of the path in feet. For example, a path 4 feet wide requires 86 cubic feet of gravel, as you can check.
(a)
If the neighbor donates 60 cubic feet of gravel, how wide a path can they build? Set up and solve a quadratic equation to find the answer in feet, accurate to two decimal places. Then convert your answer into inches.
(b)
Gravel is measured by the yard, which is short for cubic yard. There are 27 cubic feet in 1 yard of gravel. If the neighbor donates three yards of gravel, how wide a path can they build? Set up and solve a quadratic equation to find the answer in feet, accurate to two decimal places. Then convert your answer into inches.
(c)
What would it mean to solve the equation to find where \(G=0\text{?}\) Can you tell what the answer is from the equation (without actually solving)?
5.
Claude is an excellent juggler. Remember that the height \(H\) feet of Claude’s beanbag \(T\) seconds after he throws it in the air is described by the equation \(H = 3+15T-16T^2\text{.}\) Answer each of the following question by the suggested method and then look back at the graph from earlier to make sure your answers make sense.
(a)
Use the Quadratic Formula to find when the bean bag is 5 feet above ground. Why do both answers make sense in the story?
(b)
When is the beanbag 8 feet above ground? Try to use the Quadratic Formula to find the answer. What happens? Explain why it makes sense in the story that you can’t solve this quadratic equation.
(c)
Claude decided that the beanbag was too high in the air, so he modified his throw slightly. Now the height is given by \(H = 3+14T-16T^2\text{.}\) What is the maximum height the beanbag will reach now? Hint: what number can you evaluate at?
6.
The stopping distance for Jeff’s Cadillac Escalade is given by
\begin{equation*}
D=0.04S^2+1.47S
\end{equation*}
where \(S\) is the speed of the car (in miles per hour) and \(D\) is the stopping distance (in feet). Jeff took 183 feet to stop. How fast was he going?
(a)
Use successive approximation to estimate the answer to the nearest miles per hour. Display your work in a table.
(b)
Show how to use the Quadratic Formula to solve the equation.
7.
A company produces backpacks. The more they make, the less it costs for each one. The cost per backpack is given by the equation
\begin{equation*}
C = 0.01B^2 -1.2B + 50
\end{equation*}
where \(C=\) cost per backpack ($ per backpack) and \(B=\) number of backpacks.
(a)
How many backpacks do they need to produce in order to hold costs to $20/backpack? Set up and solve a quadratic equation to find the answer.
(b)
Make a table of values and draw a graph of the function. Does your answer agree with your table and graph?
(c)
What is the minimum price per backpack? Hint: evaluate at \(T= \frac{-b}{2a}\text{.}\)
8.
Mrs. Weber’s cooking class came up with the equation
\begin{equation*}
M = 1.2F^2+4F+7
\end{equation*}
to approximate the grilling time of a piece of fish depending on its thickness. Here \(M\) is the number of minutes to grill the fish and \(F\) is the thickness of the fish in inches.
(a)
If we want to make sure the fish will cook in under 20 minutes, how thick can the fish be? Set up and solve a quadratic equation to find the answer.
(b)
Repeat for 10 minutes.
9.
(a)
The company decided to declare bankruptcy when sales fell below $20 billion. In what year was that? Show how to solve using the Quadratic Formula.
(b)
An analyst had suggested that they close down shop earlier, once sales were below $50 billion. In what year did sales fall that low? Show how to solve using the Quadratic Formula.
(c)
What year did sales peak (reach their highest value)?
10.
A kangaroo hops up in the air (and out) from a 10 foot cliff. Her height above the ground, \(K\) feet, after \(T\) seconds is given by the equation
\begin{equation*}
K = 10 + 5.2T - 4.88T^2
\end{equation*}
(a)
Calculate the missing values in the table.
| T | 0 | 0.3 | 0.6 | 0.9 | 1.2 | 1.5 |
| K | 10 | 11.1208 | 11.3632 | 6.82 |
(b)
According to this equation, how high up in the air does the kangaroo get? Choose the appropriate value to plug into the equation.
(c)
When does the kangaroo land on the ground? Set up and solve an equation.
(d)
If she jumps up, but not out, when will she land on the cliff itself again, assuming the same equation holds?
