My grandmother was born in eastern Europe at the end of the 1800s. When she was eight years old her parents brought her and her younger sister and brother to the United States to escape harsh treatment by the government. Both her parents had to work, so my grandmother dropped out of school when she was thirteen years old to take care of the children, which now included another brother and sister.
Time passed and she married a handsome young veteran of World War I, who had also immigrated to the country as a young child. For her wedding dowry his parents bought my grandmother a set of sterling silverware, valued at $800 in 1920. My grandmother was very proud of her sterling and used it often.
Over the years, the sterling has increased in value, let’s say by around 3% per year. In 1957, my grandmother handed it down to my mother as a wedding present. In 1990, I married and my mother handed the sterling down to me. What was it worth at those times, and how much should it be insured for through 2015?
Let’s write the equation to answer these questions. The variables should be
\begin{align*}
S \amp= \text{ value of sterling (\$) } \sim \text{ dep} \\
Y \amp= \text{ time (years since 1920) } \sim \text{ indep}
\end{align*}
We’re saying that the sterling increased 3% per year in value. For example, in 1921, the sterling was worth
\begin{equation*}
\$800 + 3\% \text{ of } \$800 = 800 + 0.03 \times 800 = 800 + 24= \$824
\end{equation*}
Remember the shortcut here?
\begin{equation*}
800 \times 1.03 = 824
\end{equation*}
The idea is after one year we have the original $800 plus 3% more for a grand total of 103% of what we had before. And 103% = 1.03.
After 5 years, the sterling was worth
\begin{equation*}
800 \ast 1.03 \ast 1.03 \ast 1.03 \ast 1.03 \ast 1.03 = 800 \ast 1.03^5
\end{equation*}
since multiplying by 1.03 five times is the same as multiplying by \(1.03^5\text{.}\) On the calculator we do
\begin{equation*}
800 \times 1.03 \wedge 5 = 927.4192594 \approx \$927
\end{equation*}
Generalizing, we get our equation
\begin{equation*}
800 \times 1.03 \wedge Y= S
\end{equation*}
which can be rewritten as
\begin{equation*}
S=800 \ast 1.03 ^ Y
\end{equation*}
This equation fits our template for an exponential equation
\begin{equation*}
\text{dep }=\text{ start } \ast \text{growth factor}^{\text{indep}}
\end{equation*}
Quick recap. A function is
exponential if it corresponds to a fixed percent increase (or decrease). The percent increase is the
growth rate; in our example, the growth rate is
\(r=3\%=0.03\text{.}\) The number we multiply by is the
growth factor and it is also the base of the power in the equation; in our example, the growth factor is
\(g = 1.03\text{.}\) The
Percent Change Formula from Section 2.2 reminds us that
\begin{equation*}
g=1 + r = 1+0.03 =1.03
\end{equation*}
Let’s answer those questions. In 1957, we had \(Y = 1957 - 1920 = 37\) years and so
\begin{equation*}
S = 800\ast1.03^{37} = 800 \times 1.03 \wedge \underline{37}= 2388.18134\ldots \approx \$2{,}388
\end{equation*}
By 1990, we had \(Y = 1990 - 1920 = 70\) years and so
\begin{equation*}
S = 800\ast1.03^{70} = 800 \times 1.03 \wedge \underline{70}= 6334.2575\ldots \approx \$6{,}334
\end{equation*}
By 2015, we have \(Y = 2015 - 1920 = 95\) years and so
\begin{equation*}
S = 800\ast1.03^{95} = 800 \times 1.03 \wedge \underline{95}= 13262.5286\ldots \approx \$13{,}262
\end{equation*}
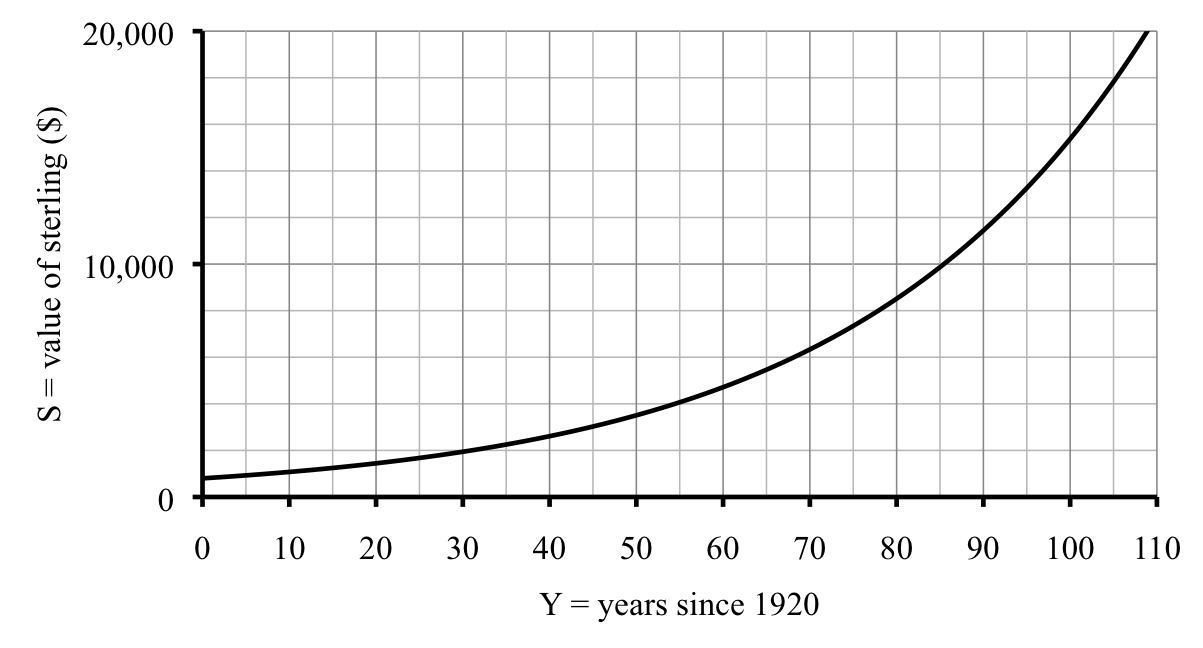
Let’s summarize this information in a table and draw a graph.
| year |
1920 |
1921 |
1925 |
1957 |
1990 |
2015 |
| \(Y\) |
0 |
1 |
5 |
37 |
70 |
95 |
| \(S\) |
800 |
824 |
927 |
2,388 |
6,334 |
13,262 |
Actually, the insurance policy allows for up to $20,000. The curve we drew suggests that the value will be $20,000 just past
\(Y=100\) (the year 2020), probably somewhere around
\(Y=110\) (the year 2030).
We can use successive approximation to improve our answer.
| year |
2020 |
2030 |
2029 |
2028 |
| \(Y\) |
100 |
110 |
109 |
108 |
| \(S\) |
15,375 |
20,663 |
20,061 |
19,476 |
| vs. 20,000 |
low |
high |
high |
low |
Seems to be around the year 2029, where
\(Y=109\text{,}\) as we had guessed.
Of course, we can solve the exponential equation instead. To find when \(S= 20{,}000\) we use our equation \(S = 800 \ast 1.03^Y\) to get
\begin{equation*}
800 \ast 1.03^Y = 20{,}000
\end{equation*}
Divide each side by 800 to get
\begin{equation*}
\frac{\cancel{800} \ast 1.03^Y}{\cancel{800}} = \frac{ 20{,}000}{800}
\end{equation*}
and so
\begin{equation*}
1.03^Y = \frac{ 20{,}000}{800} = 20{,}000 \div {800} = 25
\end{equation*}
Since we want to solve for the exponent, we use the
Log-Divides Formula with growth factor
\(g=1.03\) and the value
\(v= 25\) to get
\begin{equation*}
Y = \frac{\log (v)}{\log(g)} = \frac{\log (25)}{\log(1.03)} = \log (25) \div \log (1.03) = 108.89737 \approx 109
\end{equation*}
We rounded up to make sure it would reach the full $20,000. Since 1920 + 109 = 2029, we see (again) that the value should reach $20,000 in the year 2029.
As an aside, look what happens when we calculate the rate of change for this function. For example, during the first five years,
\begin{equation*}
\text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{\$927 - \$800}{1925-1920}= \frac{\$127}{5 \text{ years}} = 127 \div 5 = \$25.40\text{/year}
\end{equation*}
and from 1925 to 1957,
\begin{equation*}
\text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{\$2{,}388 - \$927}{1957-1925}= \frac{\$1{,}461}{32 \text{ years}} = 1{,}461 \div 32 \approx \$45.66\text{/year}
\end{equation*}
In the first few years, the value increased an average of $25.40 a year, but from 1925 to 1957 it increased an average of about $45.66 per year.
Were we supposed to get different numbers here? Well, the graph’s not a straight line and it’s not a linear equation. That tells us the rate of change isn’t going to be constant. So, sure, different numbers are fine. Does it make sense that the rate of change would itself increase? That the value increases at an increasing rate? Yes. Although we are always just adding on 3%, we’re taking 3% of larger numbers each year. So more is added each year.