It is 2:00 a.m. and Joe is up studying. The dorm has quieted down, but Joe’s feeling mighty jittery. He drank 5 large mugs of coffee in the past few hours and all that caffeine is peaking in his system now. At around 200 mg per mug, Joe wonders when his caffeine levels will drop down to where he can sleep a little.
First things first: staying up that late to study is probably a bad idea. I mean, who can think properly at 2:00 in the morning? And, how tired is Joe going to be by the time his test rolls around? Plus, we know that
\begin{equation*}
5 \text{ mugs} \ast \frac{200 \text{ mg}}{\text{mug}} = 5 \times 200 = 1{,}000\text{ mg}
\end{equation*}
which is a lot of caffeine, probably more than he needed to stay awake.
At this point Joe is stuck so let’s help him. Let’s say that at 2:00 a.m. he has 1,000 mg of caffeine in his blood. Joe searches online and discovers that 13% of the caffeine should leave his body each hour and below 300 mg he should be fine. When will that happen?
We know how percent increase works, but here the caffeine is leaving his body according to a percent decrease. I guess we need to figure it out one step at a time. After one hour (by 3:00 a.m.), Joe will have
\begin{equation*}
1{,}000 \text{ mg} - 13 \% \text{ of } 1{,}000 \text{ mg} = 1{,}000- 0.13 \times 1{,}000 = 1{,}000 - 130 = 870 \text{ mg}
\end{equation*}
By 4:00 a.m. (after 2 hours), Joe will have
\begin{equation*}
870 \text{ mg} - 13 \% \text{ of } 870 \text{ mg} = 870 - 0.13 \times 870 = 870 - 113.1 = 756.9 \text{ mg}
\end{equation*}
Wait a minute. When we calculated 13% decrease on 1,000 mg we got 870 mg. That’s 87% of 1,000. Yeah, that’s right, take off 13% and you should be left with 87% of what you started with because \(100\% - 13\% = 87\%\text{.}\) So we could have calculated
\begin{equation*}
1{,}000 \times 0.87 = 870 \text{ mg}
\end{equation*}
and then
\begin{equation*}
870 \times 0.87 = 756.9 \text{ mg}
\end{equation*}
Aha, to find the amount after a 13% decrease we just multiply by 0.87.
Still nowhere near 300 mg so fast-forward. For example, after 5 hours (at 7:00 a.m.), we need to multiply 1,000 by 0.87 five times
\begin{equation*}
1000 \ast 0.87 \ast 0.87 \ast 0.87 \ast 0.87 \ast 0.87= 1{,}000 \ast 0.87^5
\end{equation*}
where we use a power to abbreviate repeatedly multiplying. So
\begin{equation*}
1000 \ast 0.87^5 = 1{,}000 \times 0.87 \wedge 5 = 498.420920\ldots \approx 498.4 \text{ mg}
\end{equation*}
The bad news is that it’s 7:00 a.m. and Joe is still too jittery to sleep. The good news is that we can write the equation. The variables are
\begin{align*}
J \amp= \text{ Joe's caffeine level (mg) } \sim \text{ dep} \\
H \amp= \text{ time (hours since 2:00 a.m.) } \sim \text{ indep}
\end{align*}
Our equation must be
\begin{equation*}
J = 1{,}000 \ast0.87^H
\end{equation*}
Notice this equation fits our template for an exponential equation.
\begin{equation*}
\text{dep }=\text{ start } \ast \text{growth factor}^{\text{indep}}
\end{equation*}
A little terminology here. When a function is exponential but decreasing, it’s called
exponential decay. It sounds a little odd to say “growth factor” if the quantity is getting smaller so we sometimes say
decay factor instead. We know from the
Percent Change Formula that the growth factor (
\(g\)) can be found from the growth rate (r) by the formula
\(g=1+r\text{.}\) If we think of 13% decrease as negative growth rate,
\(r=-13\%=-0.13\text{,}\) then the formula still works to find the decay factor (
\(g\))
\begin{equation*}
g= 1 + r = 1 + -0.13 = 1-0.13 = 0.87
\end{equation*}
Back to jittery Joe. Let’s summarize what we’ve found and add a few more times to see when Joe’s caffeine level should fall below 300 mg.
| time |
2:00 |
3:00 |
4:00 |
5:00 |
6:00 |
7:00 |
8:00 |
9:00 |
10:00 |
11:00 |
| \(H\) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| \(J\) |
1,000 |
870 |
756.9 |
658.5 |
572.9 |
498.4 |
433.6 |
377.3 |
328.2 |
285.5 |
| vs. 300 |
high |
high |
high |
high |
high |
high |
high |
high |
high |
low |
That means Joe should be able to fall asleep by around 11:00 a.m. Exactly when his exam starts. Sorry, Joe.
We could have solved the equation instead. We were looking for \(J = 300\text{.}\) Using our equation \(J = 1{,}000 \ast 0.87^H\) we get
\begin{equation*}
1{,}000 \ast 0.87^H=300
\end{equation*}
Divide each side by 1,000 to get
\begin{equation*}
\frac{\cancel{1{,}000} \ast 0.87^H}{\cancel{1{,}000}}= \frac{300}{1{,}000}
\end{equation*}
which simplifies to
\begin{equation*}
0.87^H = \frac{300}{1{,}000} = 300 \div 1{,}000 = 0.3
\end{equation*}
We find ourselves in the familiar situation – solving to find the exponent. Logs to the rescue. By the
Log-Divides Formula with growth factor
\(g=0.87\) and value
\(v= 0.3\) we get
\begin{equation*}
Y = \frac{\log (v)}{\log(g)}= \frac{\log (0.3)}{\log(0.87)} = \log (0.3) \div \log (0.87) = 8.64537506\ldots \approx 9
\end{equation*}
which corresponds to 11:00 a.m. Same answer. Much quicker.
Quick side note. We could have rounded to 8.64 hours and then converted units to get
\begin{equation*}
0.64 \text{ hours} \ast \frac{60 \text{ minutes}}{1 \text{ hour}} = 0.64 \times 60 = 38.4 \approx 39 \text{ minutes}
\end{equation*}
Counting from 2:00 a.m., we see that Joe’s caffeine levels drop below 300 mg at 10:39 a.m. Since we are approximating throughout the problem, we should round to 11:00 a.m. anyway.
Let’s calculate the rate of change and think about what it means. During the first hour,
\begin{equation*}
\text{rate of change} = \frac{\text{change dep}}{\text{change indep}}
= \frac{870\text{ mg}-1{,}000\text{ mg}}{\text{3:00 a.m.} - \text{2:00 a.m.}}
= \frac{-130 \text{ mg}}{1 \text{ hour}}
= -130 \text{ mg/hour}
\end{equation*}
Was the rate of change supposed to be negative? Sure. Joe’s caffeine level is dropping. Any decreasing function has a negative rate of change. And, as exam time approaches,
\begin{equation*}
\text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{285.5\text{ mg}-328.2 \text{ mg}}{\text{11:00 a.m.} - \text{10:00 a.m.}} = \frac{-42.7 \text{ mg}}{1 \text{ hour}} \approx -43 \text{ mg/hour}
\end{equation*}
Joe’s caffeine level was dropping faster at first and is not dropping as fast now.
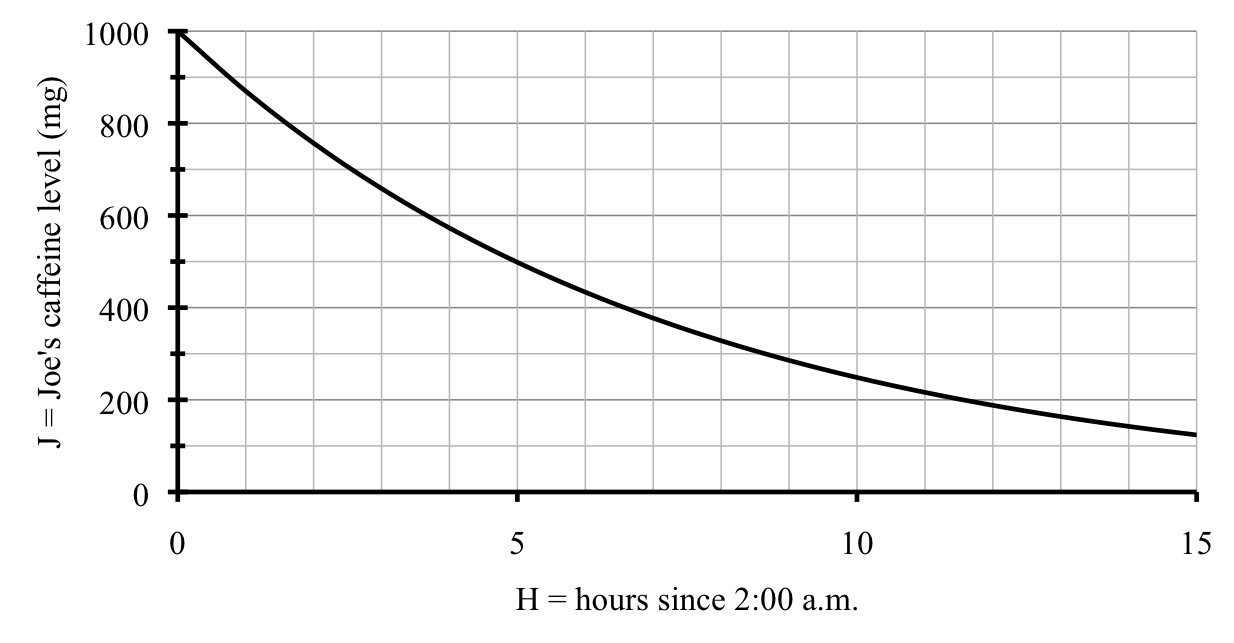
A glance at the graph confirms our findings.
One last thing. There’s another way to describe the decrease here. When our story began Joe’s caffeine level was around 1,000 mg and after 5 hours it was at 498.4 mg. That’s just about 500 mg, or
half of what he started with. We say the
half-life of caffeine is around 5 hours.
Doesn’t sound very important but check this out. Start with 1,000 mg. After 5 hours, there’s 500 mg left. (Okay, approximately.) Now go another 5 hours, which means 10 hours total. Evaluate our equation \(J = 1{,}000 \ast 0.87^H\) when \(H =10\) to get
\begin{equation*}
J = 1{,}000 \ast 0.87^{10} = 1{,}000 \ast 0.87 \wedge \underline{10} = 248.423414\ldots \approx 250 \text{ mg}
\end{equation*}
That means half of what was left is now gone. Go another 5 hours. Lose another half. Check for yourself:
\begin{equation*}
J = 1{,}000 \ast 0.87^{15} = 1{,}000 \ast 0.87 \wedge \underline{15} = 123.819426\ldots \approx 125 \text{ mg}
\end{equation*}
And so on. Cool.