In the United States temperatures for everyday things like the weather or cooking are given in Fahrenheit, denoted °F. In this system, water freezes into ice at 32°F and boils into steam at 212°F. A common setting for room temperature is 68°F whereas average human body temperature is around 98.6°F. And, most importantly, chocolate brownies bake at 350°F.
In the sciences, medicine, and most other countries, temperatures are measured in Celsius, denoted °C. (For those of us who grew up in the 1960s or earlier, “Celsius” is the temperature scale formerly known as “centigrade.”) For comparison’s sake, it’s useful to know that water freezes at 0°C and boils at 100°C. Not coincidentally - it was set up that way. Room temperature is 20°C whereas now average human body temperature is 37°C. And those brownies?
A common conversion is given by the equation
\begin{equation*}
F = 1.8C+32
\end{equation*}
where
\begin{align*}
F \amp= \text{ Fahrenheit temperature (}^\circ \text{F) } \sim \text{ dep} \\
C \amp= \text{ Celsius temperature (}^\circ \text{C) } \sim \text{ indep}
\end{align*}
You may have seen this equation before with fractions in it: \(F = \frac{9}{5}C + 32\text{.}\) Just another way to write the equation, since \(\frac{9}{5} = 9 \div 5 = 1.8\text{.}\) For example, when \(C=100\) we have
\begin{equation*}
F= 1.8 \ast 100 + 32 =1.8 \times \underline{100}+32= 212 \quad \checkmark
\end{equation*}
You can (and should check) the other examples in our story.
What about those chocolate brownies? We are looking for
\(F=350\text{.}\) That’s the dependent variable, so you can practice your linear equation solving skills to find the independent variable,
\(C\text{.}\) It turns out that chocolate brownies bake at around 177°C.
But, actually, chocolate brownies just need to bake in a moderate oven, which means between 325°F and 375°F. Let’s first figure out when the oven temperature is under 375°F. We want to know when
\begin{equation*}
F \le 375
\end{equation*}
so we have an inequality instead of an equation. Remember \(\le\) stands for less than or equal to. Using \(F=1.8C+32\) we get
\begin{equation*}
1.8C+32 \le 375
\end{equation*}
We’re looking for values of \(C\) that make the left-hand side a number that’s smaller than, or maybe as large as, 375, but no larger.
Quick vocabulary: equations have equal signs (=). When we have inequality signs (
\(\le\text{,}\) \(\ge\text{,}\) \(\gt\text{,}\) or
\(\lt\)), it’s called an
inequality instead.
To solve this inequality we begin the same way as we would if we were solving the equation, by subtracting 32 from each side to get
\begin{alignat*}{2}
1.8C + \cancel{32} \amp \leq \amp 375 \\
-\cancel{32} \amp \amp -32
\end{alignat*}
which simplifes to
\begin{equation*}
1.8C\le375-32=343
\end{equation*}
To understand why the inequality stays the same when we subtract, think of the inequality as “little”
\(\le\) “big.” If one number is smaller than the other, the same will be true if we subtract the same amount from each number. For example,
\(18 \le 21\text{.}\) To make it real, suppose I have $18 and you have $21. Then imagine we each buy a movie ticket for $12. I would have
\(\$18-\$12 = \$6\) and you would have
\(\$21-\$12 = \$9\text{.}\) And still
\(6 \le 9\text{.}\)
Back to our example. We had \(1.8C\le343\text{.}\) Divide each side by 1.8 to get
\begin{equation*}
\frac{\cancel{1.8}C}{\cancel{1.8} }\le \frac{343}{1.8}
\end{equation*}
which simplifies to
\begin{equation*}
C\le \frac{343}{1.8}= 343 \div 1.8 = 190.555555\ldots \approx 190^\circ C
\end{equation*}
The oven should be set at most 190°C. We rounded down because we do not want the brownies to burn.
To understand why the inequality stays the same when we divide, again think of the inequality as “little”
\(\le\) “big.” If one number is littler than the other, the same will be true when we divide each number by the same divisor. For example,
\(6 \le 9\text{,}\) which we imagined as my having $6 and your having $9 after we each bought a movie ticket. While we’re making up stories, suppose we each have three children who want some money from us for treats. We each divide our remaining cash among our three children, respectively. My kids each get
\(\$6\div3 =\$2\) and your kids each get
\(\$9\div 3 = \$3\text{.}\) And
\(2 \le 3\) still.
There is a bit of caution when solving inequalities. When symbolically solving an equation, any operation you do to each side preserves the equality: start with equal amounts, do the same thing to each, end with equal amounts. But, when symbolically solving an inequality, only some operations you do to each side preserves the inequality: add or subtract from each side or multiply or divide each side by the same (positive) number. But other operations can reverse the inequality.
For example, we can swap sides of an equation, but if we swap sides of an inequality then the direction of the sign reverses. In this brownie example, we want
\begin{equation*}
F \ge 325
\end{equation*}
Remember \(\ge\) stands for greater than or equal to. That’s like “big” \(\ge\) “little.” We can rewrite that inequality as “little” \(\le\) “big,” or equivalently
\begin{equation*}
325 \le F
\end{equation*}
In each case, \(325\) is “little” and \(F\) is “big”. Make sense?
Multiplying or dividing each side of an inequality by a negative number switches the inequality sign as well. Watch out for that with decreasing functions because that’s where the slope is negative. And the number we’re dividing by is actually the slope.
Remember that the recipe for chocolate brownies says to bake in a moderate oven, between 325°F and 375°F. We just figured out that
\(F \le 375\) corresponds to
\(C \le 190\text{.}\) But that’s only half of the story. We also wanted
\(F \ge 325\text{.}\) While we could solve that inequality separately, it turns out there’s an easier way.
Inequalities are a very useful notation for indicating “between”. We want between 325°F and 375°F to bake the brownies. We can write
\begin{equation*}
325 \le F \le 375
\end{equation*}
which is read
“
\(F\) is between 325 and 375 (inclusive)”
The word
inclusive indicates that we’re allowing
\(F=325\) or
\(F=375\text{.}\)
The good news is that we can solve this chain of inequalities all at once using the same steps as before but now being sure to do the same thing to all three sides. “Three sides?” you ask. Yes, “three,” I confirm. Watch how this works. Start with
\begin{equation*}
325 \le F \le 375
\end{equation*}
Using \(F=1.8C + 32\) we get
\begin{equation*}
325 \le 1.8C + 32 \le 375
\end{equation*}
Subtract 32 from each of the three sides to get
\begin{equation*}
\begin{array} {ccc cc}
325 \amp \le \amp 1.8C + \cancel{32} \amp \le \amp 375 \\
-32 \amp\amp -\cancel{32} \amp\amp -32 \\
\end{array}
\end{equation*}
which simplifies to
\begin{equation*}
293 \le 1.8C \le 343
\end{equation*}
Next, divide all three sides by 1.8 to get
\begin{equation*}
\dfrac{293}{1.8} \leq
\dfrac{\cancel{1.8}C}{\cancel{1.8}} \leq
\dfrac{343}{1.8}
\end{equation*}
which simplifies to
\begin{equation*}
293\div 1.8 \le C \le 343 \div 1.8
\end{equation*}
so,
\begin{equation*}
162.777777\ldots \le C \le 190.555555\ldots
\end{equation*}
Probably best to say
\begin{equation*}
163 \le C \le 190
\end{equation*}
Chocolate brownies bake between 163°C and 190°C. Ovens actually aren’t that precise, so somewhere between 170°C and 190°C should do the job.
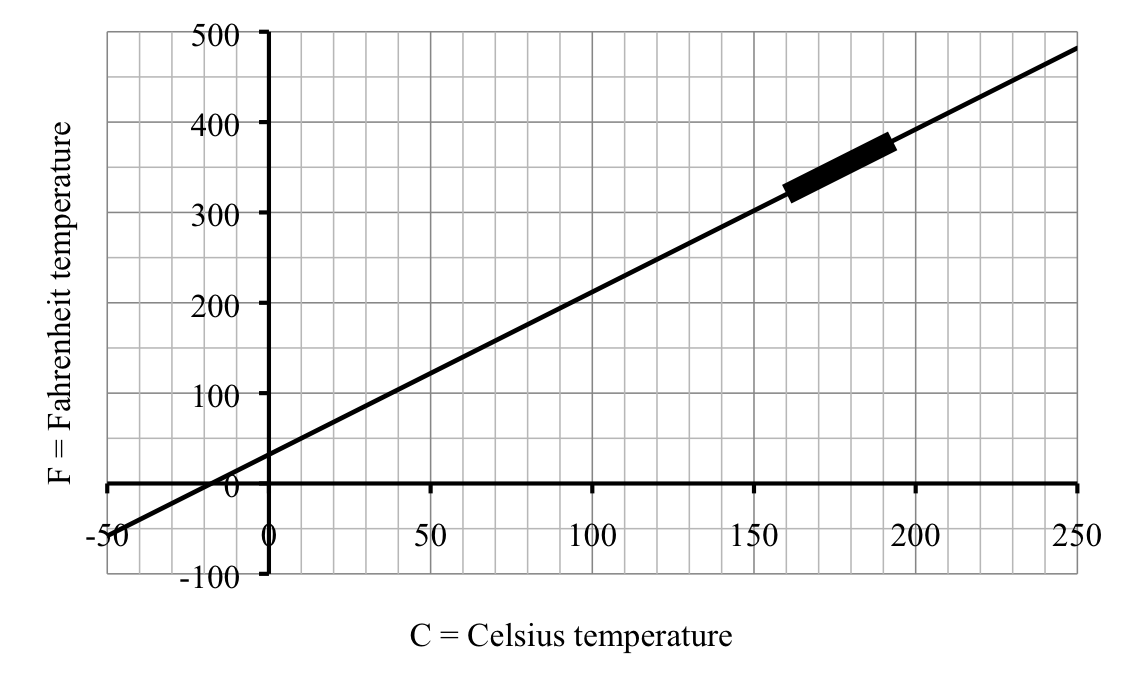
If we graph our linear function
\(F = 1.8C+32\text{,}\) we can check our answer for the right temperature range for our brownies. Since we want
\(F\) between 325 and 375 we start on the vertical axis and then use the graph to find the right range on the horizontal axis. You can see from the highlighted region that our answer is reasonable. Now, who wants brownies?