Thanh has an internship studying road salt usage in a northern metropolitan area. Road salt is used to melt ice and snow on paved streets. Because it can damage vegetation and influence both surface water (lakes) and ground water, and because it costs money to run the trucks that apply the salt, people are interested in the amount of road salt used.
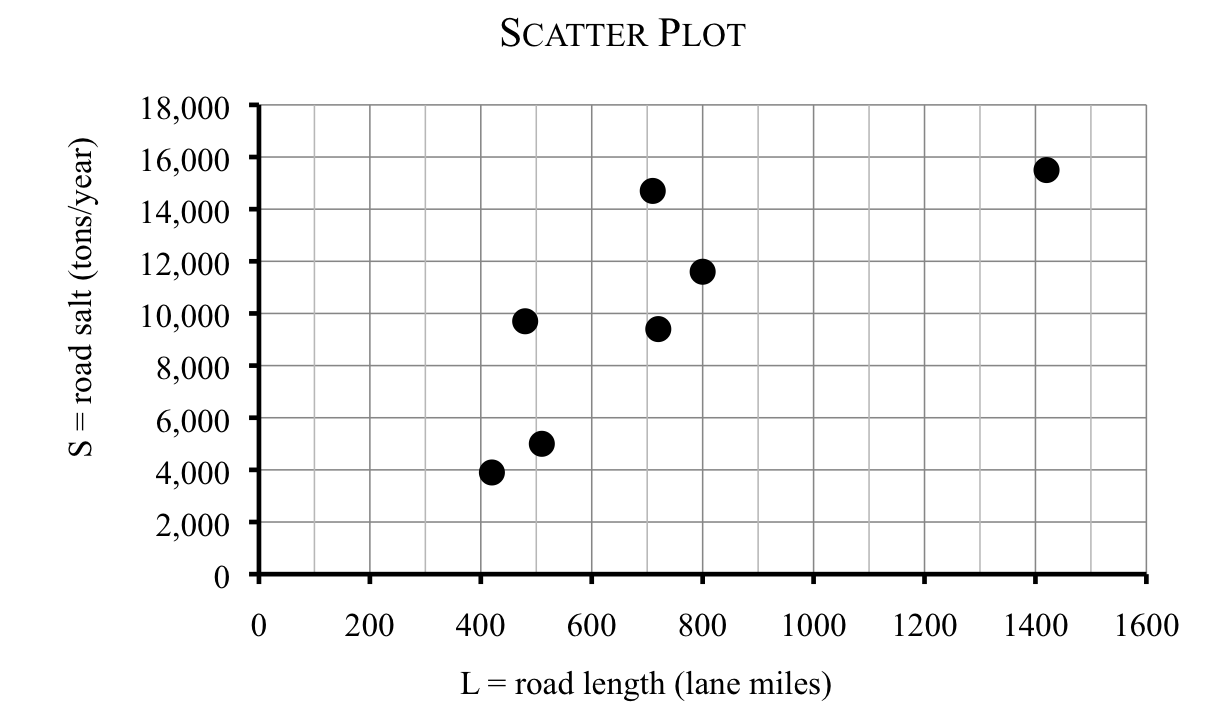
One data set compares road salt usage per county. Thanh learned from county officials that road salt use varies widely from county to county, but, not surprisingly, it depends heavily on the length of road in the county. So, the variables are
\begin{align*}
L \amp= \text{ road length (lane miles) } \sim \text{ dep} \\
S \amp= \text{ road salt applied (tons per year) } \sim \text{ indep}
\end{align*}
A lane mile is the area of road one mile long and one lane wide. Now you know.
Thanh also learned that while road salt use is a function of lane miles, it is not proportional as there are more complicated factors involved. Still, he would like to model road salt use as a function of road length. Here are the data for counties in the metro area.
| \(L\) |
710 |
420 |
800 |
1,420 |
720 |
510 |
480 |
| \(S\) |
14,700 |
3,900 |
11,600 |
15,500 |
9,400 |
5,000 |
9,700 |
To develop his model Thanh imagined a new county, County X, that had 600 lane miles of road. In looking at the data, he finds two counties with close to 600 lane miles: County T and County A.
| \(L\) |
510 |
600 |
710 |
| \(S\) |
5,000 |
? |
14,700 |
Based on this data, Thanh expects County X would use between 5,000 and 14,700 tons/year of road salt. Since 600 is closer to 510 than to 710, he starts with a guess of around 9,000 tons/year of road salt.
To improve this estimate, Thanh decides to use a linear model, hoping that will account for both road length influence and fixed factors. He begins by finding the slope.
\begin{align*}
\text{slope} \amp = \text{rate of change} = \frac{\text{change dep}}{\text{change indep}} = \frac{14{,}700\text{ tons/year}-5{,}000 \text{ tons/year}}{710\text{ lane miles}-510 \text{ lane miles}}\\
\amp = (14{,}700-5{,}000)\div(710-510)= 48.5 \text{ tons/year per lane mile}
\end{align*}
Next he calculates the intercept.
\begin{equation*}
\text{intercept} = \text{dep} -\text{slope}\ast\text{indep}= 5{,}000 - 48.5\times 510= -19{,}735 \text{ tons/year}
\end{equation*}
He was not expecting a negative value but decides to use it anyway. Using the template for a linear equation
\begin{equation*}
\text{dep} = \text{start} + \text{slope} * \text{indep}
\end{equation*}
Thanh gets
\begin{equation*}
S = -19{,}735 + 48.5L
\end{equation*}
which he rewrites as
\begin{equation*}
S = 48.5L-19{,}735
\end{equation*}
As a check, for \(L=710\) lane miles, he gets
\begin{equation*}
S=48.5 \times \underline{710}-19{,}735=14{,}700 \text{ tons/year}\quad \checkmark
\end{equation*}
More importantly, for 600 miles his equation gives the estimate of
\begin{equation*}
S=48.5 \times \underline{600}-19{,}735=9{,}365\text{ tons/year}
\end{equation*}
Thanh rounds this estimate to 9,400 tons/year of road salt for County X, which is close to his initial guess of 9,000 tons/year.
Next, Thanh imagines another new county, County Y, that has 500 lane miles of road. He looks to the data for counties with close to 500 lane miles.
| \(L\) |
480 |
500 |
510 |
| \(S\) |
9,700 |
? |
5,000 |
Wait a minute. The county with fewer roads used more salt? That doesn’t make sense.
Thanh decides to look at all the data at once in a scatter plot.
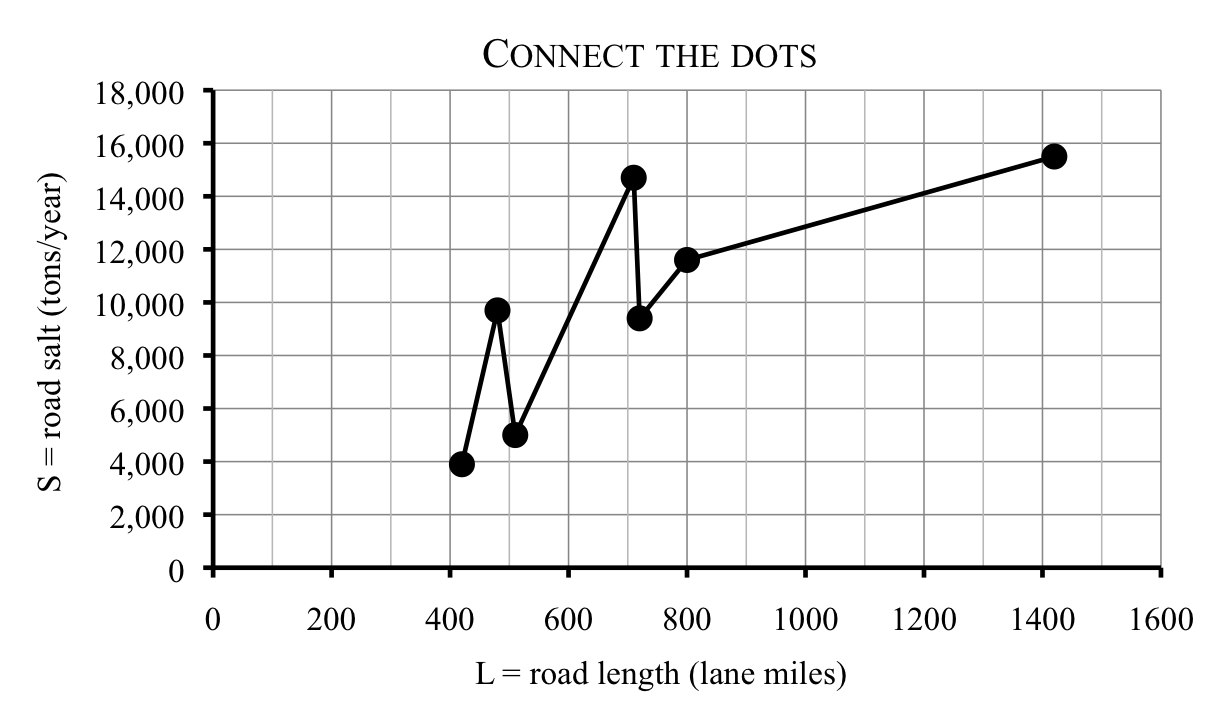
When Thanh was using the nearby points to estimate for Counties X and Y, it’s as if he were connecting the dots with line segments on the graph. Notice that the line that goes through 500 lane miles is decreasing, just like Thanh saw in his table.
Thanh suspects that this connect-the-dots model is too heavily influenced by individual county road-salting habits. He would like a way to get one line to use for everything, knowing full well that one line cannot possibly go through all of the data points.
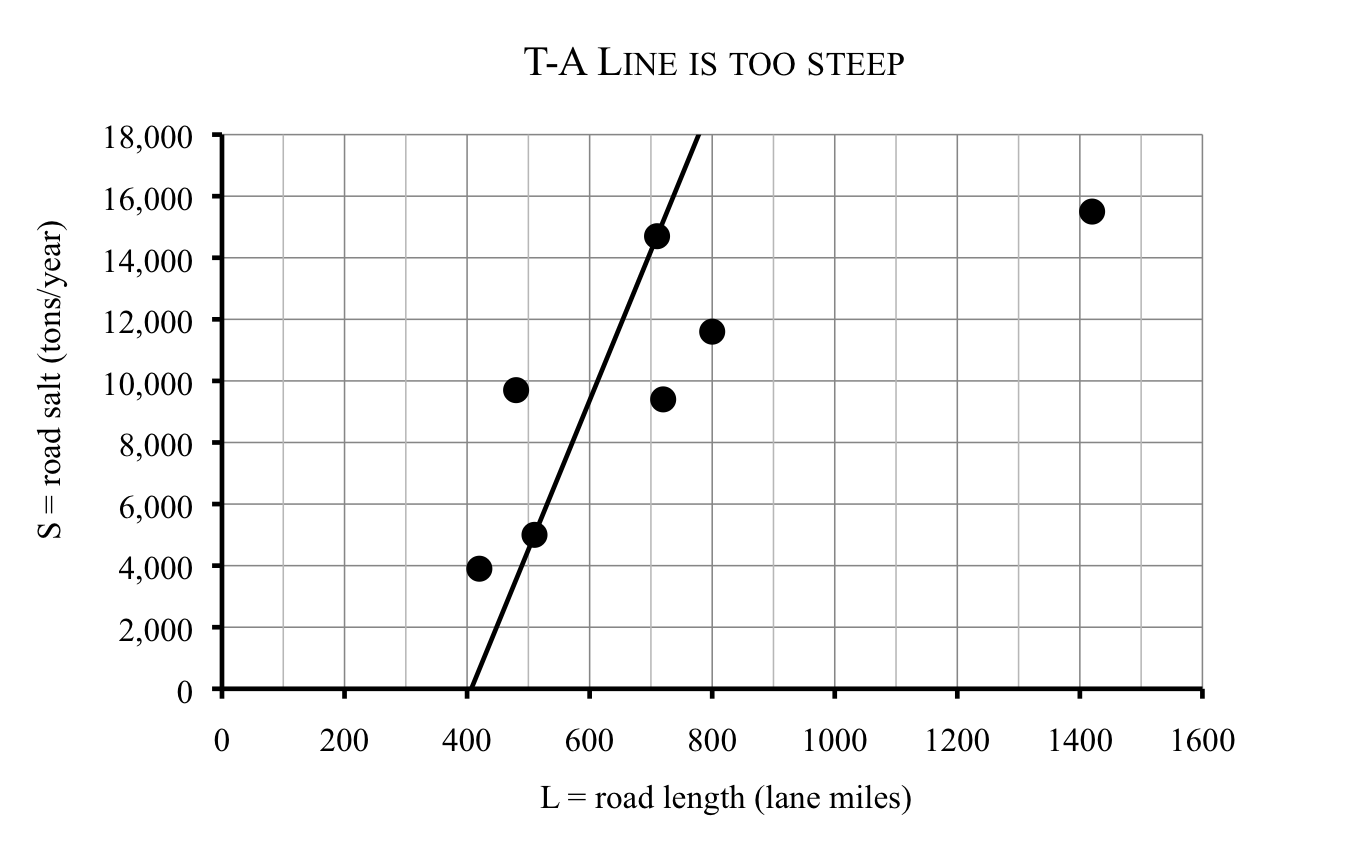
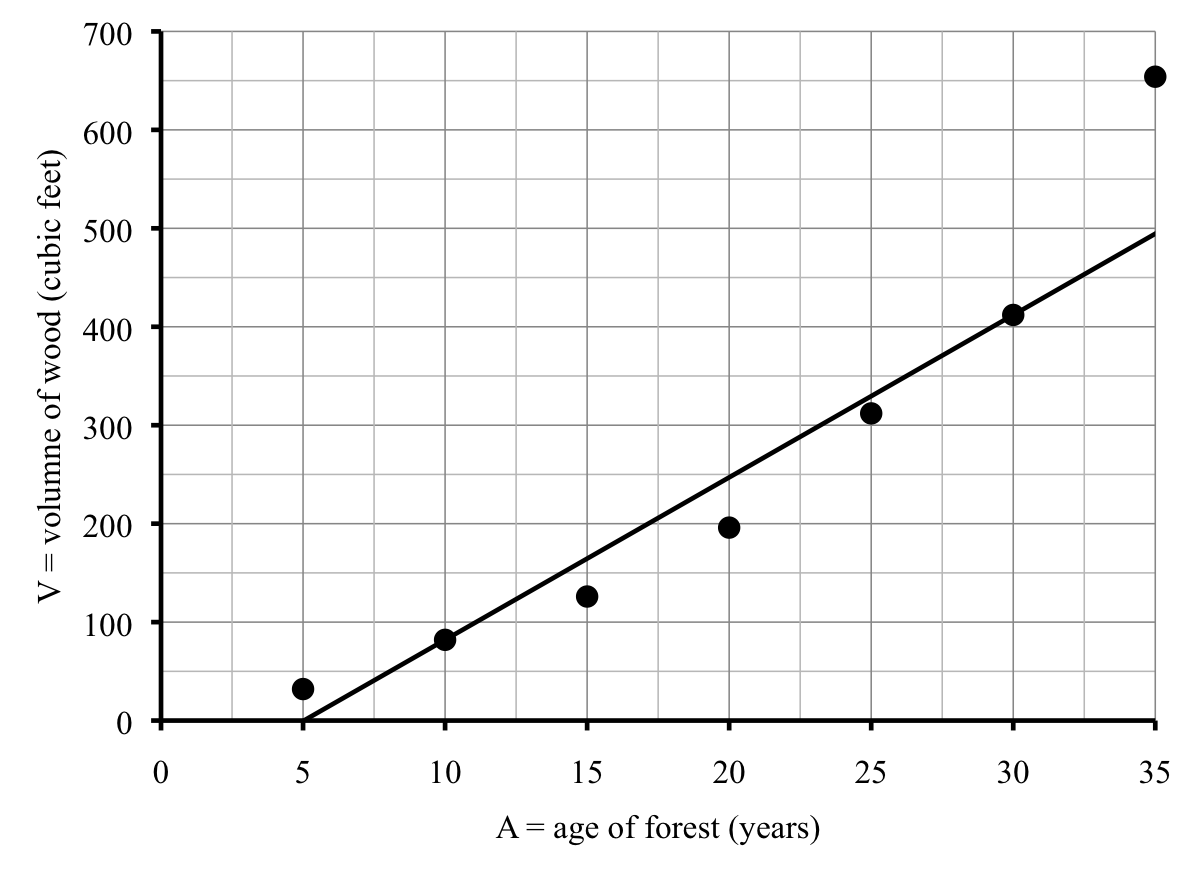
Which line to use? One option would be to stick with the line he found through the points for Counties T and A:
\begin{equation*}
\textbf{T-A line:} \quad S = 48.5L-19{,}735
\end{equation*}
He redraws the scatter plot to show that line. Because the intercept is negative, it doesn’t show up on his graph. The line seems to be too low at first and too high later. The problem is that this line is too steep (has too large a slope).
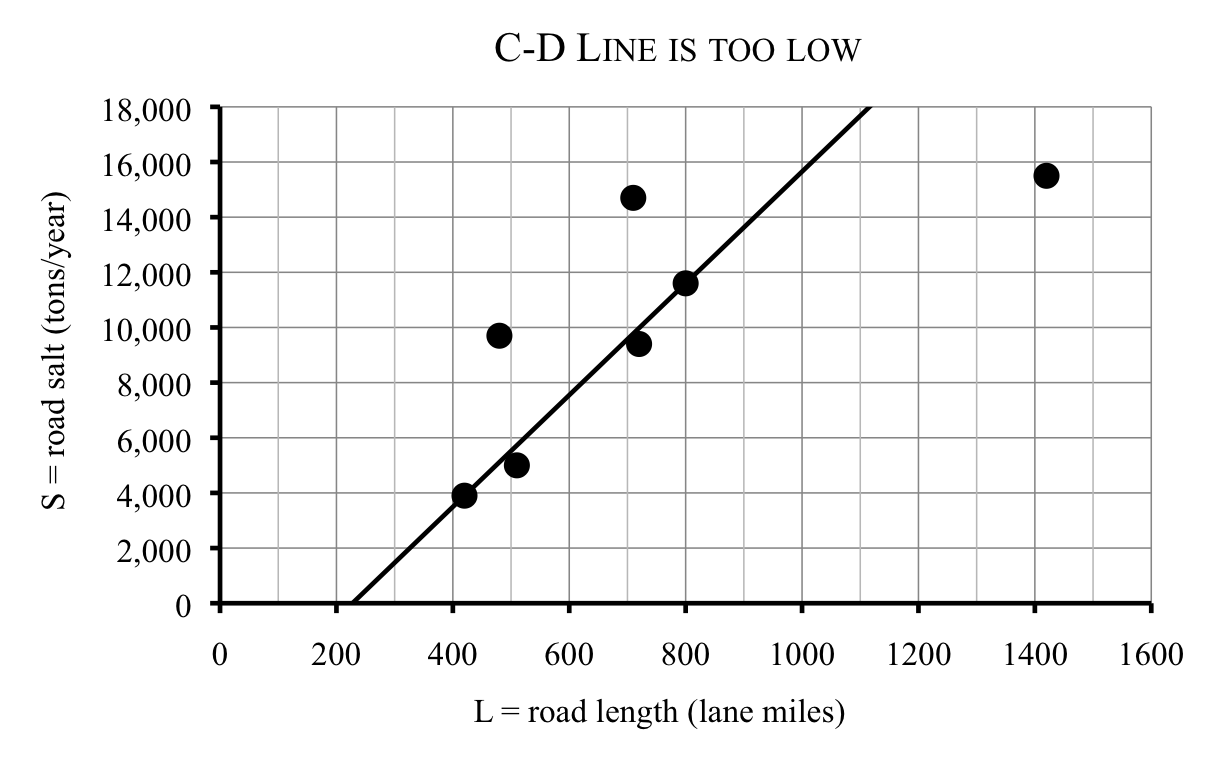
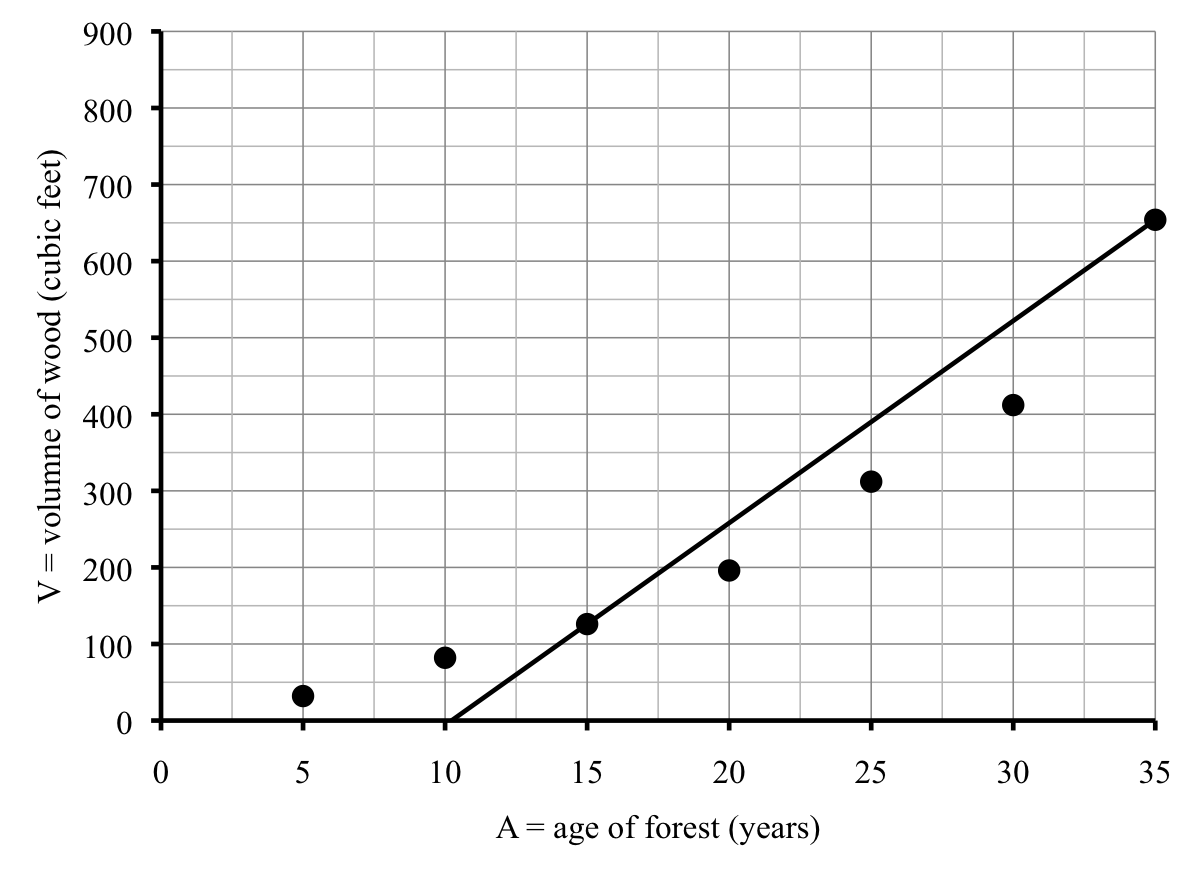
Thanh decides to try a line that is less steep. After drawing in a few lines, he decides to try the line between the points for Counties C and D instead, which has equation
\begin{equation*}
\textbf{C-D line:} \quad S = 20.26L-4{,}610
\end{equation*}
Unfortunately this line seems too low. (Again the negative intercept isn’t visible.)
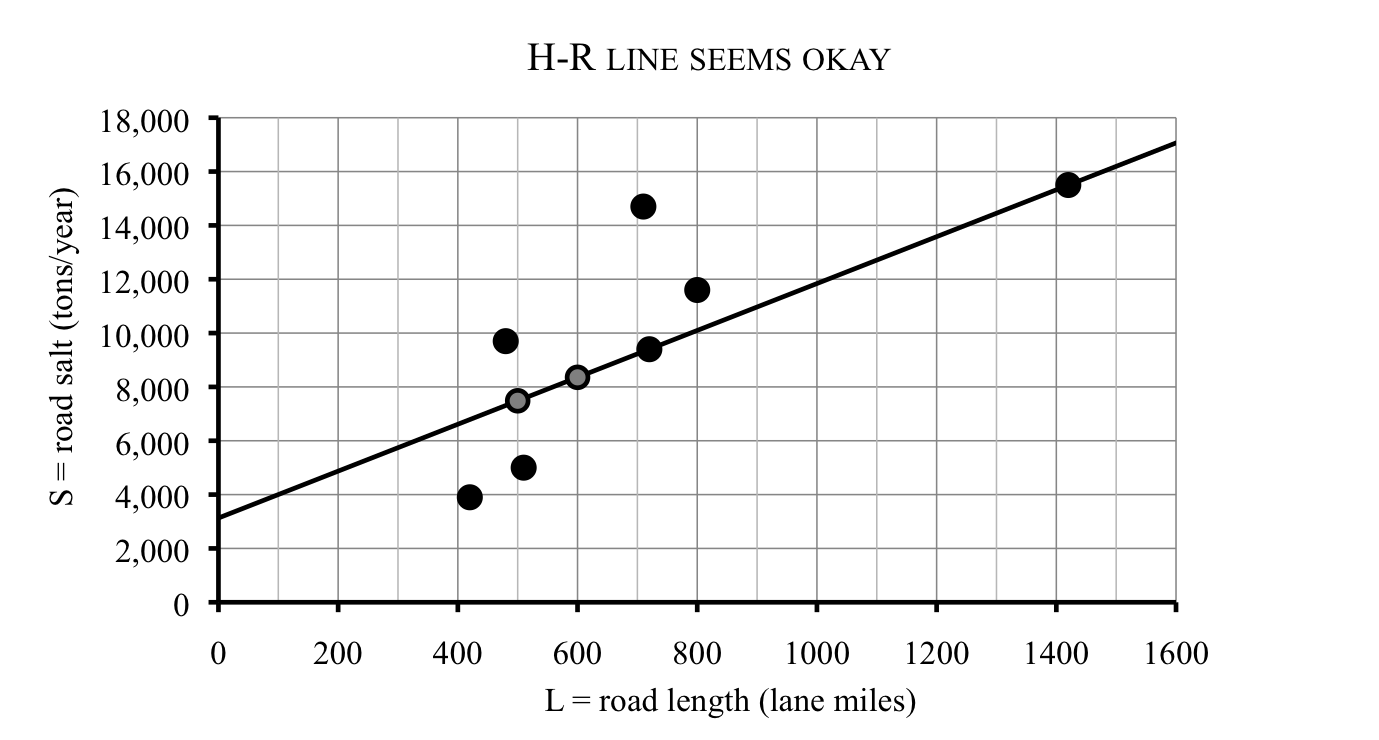
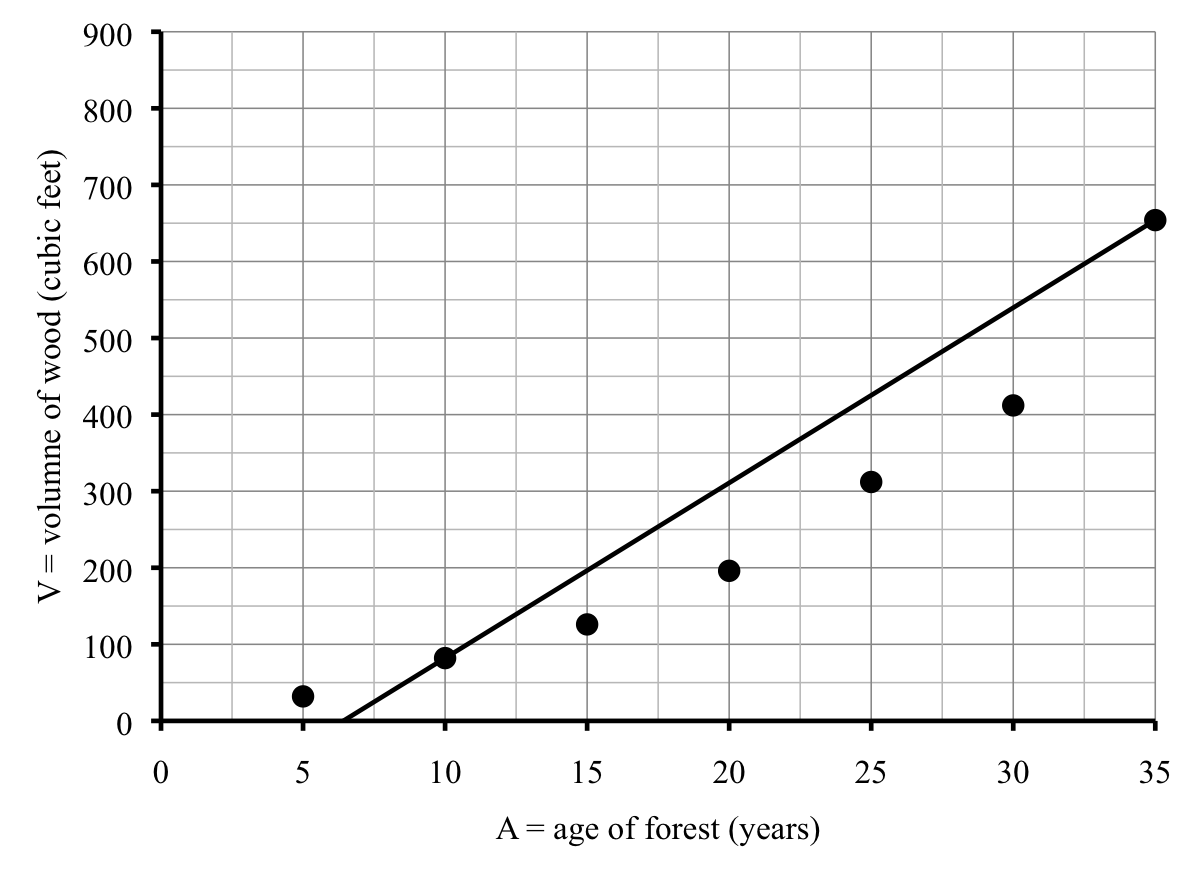
Neither of these lines came close to the point for County H on the far right, so Thanh considers one more line, this time through County H and County R, which has equation
\begin{equation*}
\textbf{H-R line:} \quad S = 8.71L+3{,}130
\end{equation*}
This line has a positive intercept just above 3,000 tons/year, as you can see on the graph.
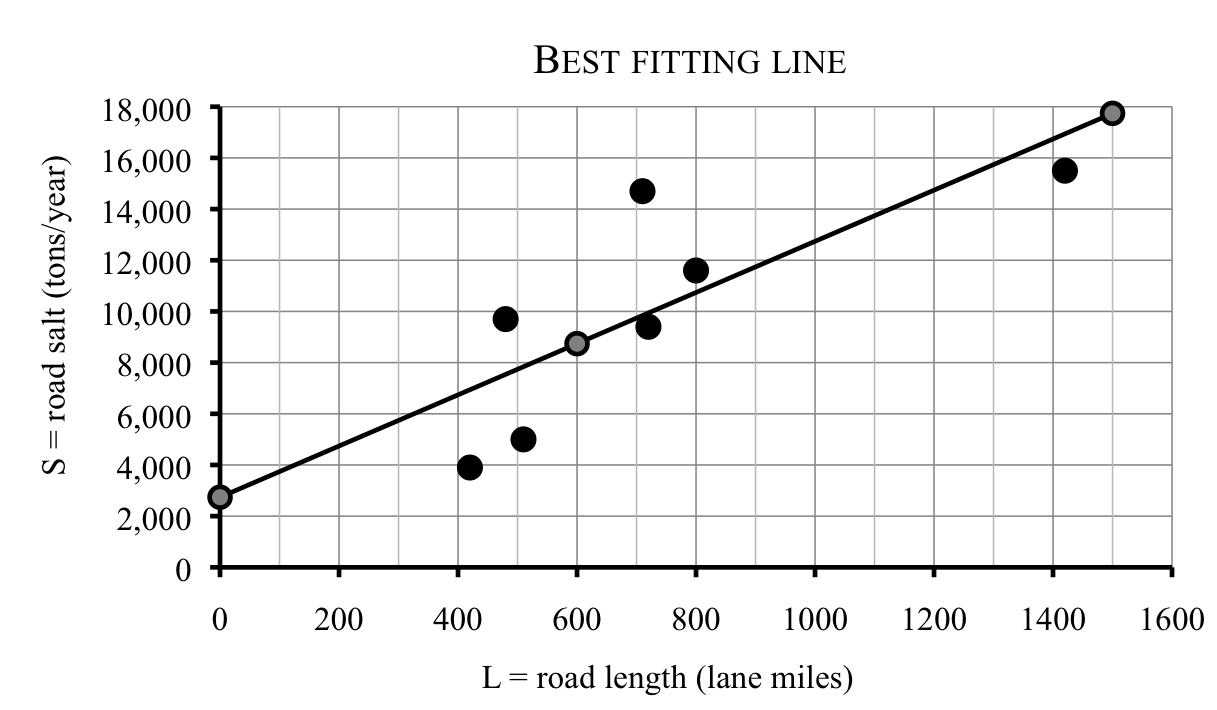
Thanh thinks the H-R line is reasonable, but it makes him wonder how to decide if one line is better than another. Generally speaking the best fitting line makes the space between the line and the data points as small as possible. (There is actually a much more official definition.) After using a little statistical software, Thanh determines that for this data set, the official best fitting line has equation
\begin{equation*}
\textbf{Best fitting line:} \quad S = 10.0L+2{,}741
\end{equation*}
Thanh wants to add this line to his graph so first he calculates a few values. While it’s true that any two points would do, he played it safe and plotted three points, being sure to use 0 in order to find the intercept.
| \(L\) |
0 |
600 |
1,500 |
| \(S\) |
2,741 |
8,741 |
17,741 |
He graphs this line and notices it is very similar to the H-R line, just a tiny bit higher and a tiny bit steeper. The points from the table are highlighted on the graph just to help you see how we graphed the line. Remember, those aren’t actual data points.
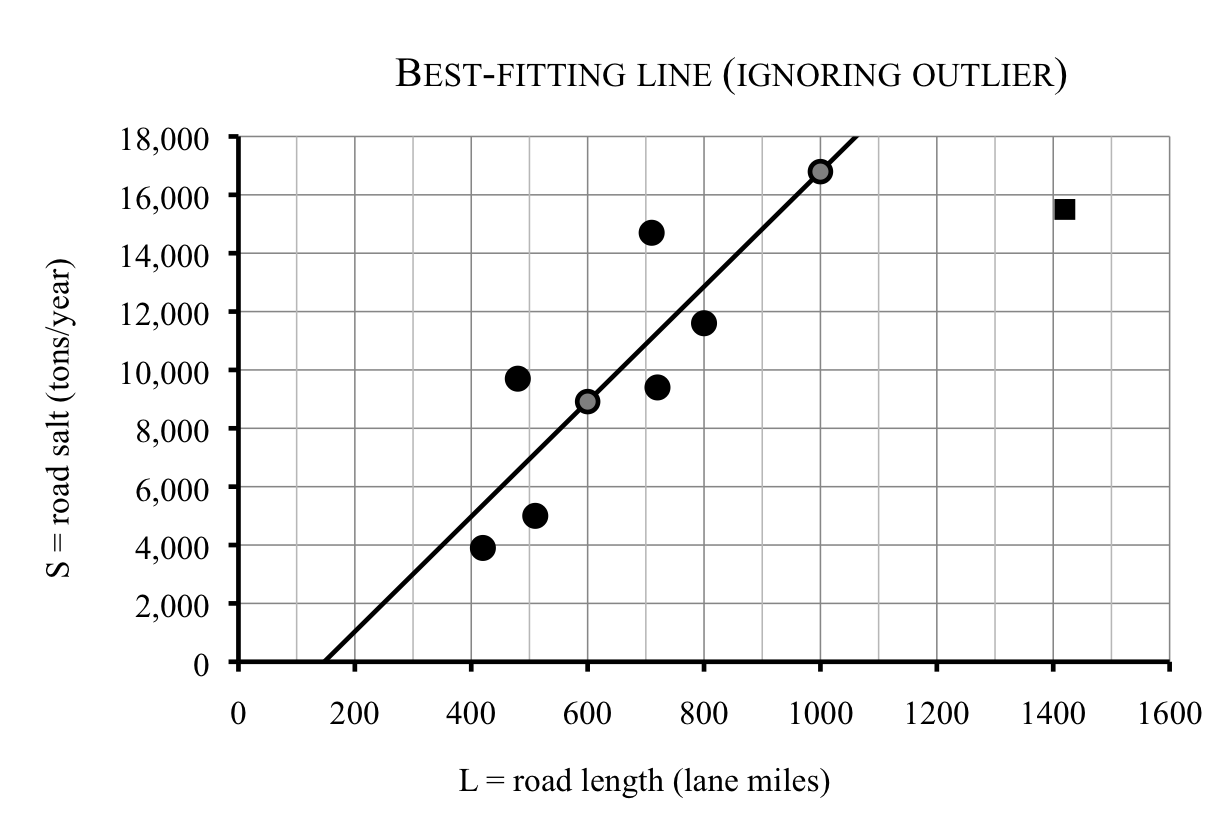
Thanh is bothered by the fact that County H seems to be off on its own. The largest city in this area is in County H. Between the budget crunch and the nature of the urban landscape, the city tends to use much less road salt than the surrounding areas. So County H really isn’t very typical at all. In statistics, this sort of value is known by the descriptive term
outlier (as in “it lies way out there.”)
So Thanh decides to look at the statistically best-fitting line ignoring County H this time. Back to his software and he finds
\begin{equation*}
\textbf{Best fitting line (ignoring outlier):} \quad S = 19.7L-2{,}905
\end{equation*}
This line is less steep than the T-A line and higher than the C-D line. Seems perfect.